Zahlwort

Vor 18 Jahren begab ich mich auf die Suche nach einem 27. Buch­sta­ben, um zusam­men mit den zehn Zif­fern auf 27·37=999 zwei­stel­lige alpha­nume­ri­sche Be­zeich­nun­gen zu kom­men. Ein paar Son­der­zei­chen, Um­laute und Liga­tu­ren schied ich aus. Damit ei­gent­lich auch die Liga­tur & aus klei­nem E und T, das Amper­sand, Et‑Zei­chen, kauf­män­ni­sches Und und mir als Krä­mer‑Und in Erin­ne­rung.

Erst später vernahm ich, daß & früher letz­ter Buch­stabe im eng­li­schen Alpha­bet war und so unter den vie­len sei­ner­zeit ge­bräuch­li­chen Liga­tu­ren eine beson­dere Stel­lung ein­nahm. Da eng­li­sche Kinder das Alpha­bet am Ende mit „x, y, z, and per se and“ auf­sag­ten, bür­ger­te sich die Be­zeich­nung Amper­sand ein.

Aber auch dieses Krä­mer‑Und schei­det für mich als 27. Buch­stabe aus. Wie Klam­mer­affe und Dol­lar ist es in der Daten­ver­arbei­tung oft­mals ein Meta­zei­chen, ins­beson­dere unter HTML. Ähn­li­ches gilt auch für andere in letz­ter Zeit in Fließ­texte ein­ge­drun­gene Zei­chen wie #, +, - und alle Satz­zei­chen. Damit ist die Suche beendet.

27 | 999 | ASCII | Unterstrich | Klammeraffe | Dollar | Eszett | Umlaute

Es ist schon erstaun­lich, was man­che alles für para­dox hal­ten, nur weil es nicht der spon­tanen nai­ven Erwar­tung ent­spricht und sie nicht in der Lage oder bereit sind, den ein­fa­chen Zusam­men­hang zu sehen oder den feh­len­den anzu­er­ken­nen.

Ein Beispiel für einen ein­fa­chen Zu­sam­men­hang: Trotz Imp­fung nimmt der Anteil der Geimpf­ten in den Kran­ken­häu­sern zu. Ja, sofern nicht ein Wun­der­mit­tel zum neu­deut­schen Nach­boostern gefunden wird, bleibt es so. In 2020 lag der Anteil Geimpf­ter bei 0 Pro­zent, jetzt bereits bei 50 und macht sich Rich­tung 100 auf, die aber dank des Wider­stan­des der Impf­gegner nur sehr schwer zu er­reichen sind.

Ein Beispiel für einen fehlen­den oder zufäl­ligen Zusam­men­hang: Wo viel geimpft wurde, sind die Inzi­den­zen hoch. Das stimmte. Einen Grund kannte ich nicht, obwohl auch nichts dagegen spricht, daß man bei fal­len­den Inzi­den­zen nachlässig wird. Ins­beson­dere im Osten, wo man sich rie­sige Fall­zahlen gönnte, fielen sie aus Angst, schlech­ter Erfah­rung, Gesichts­wah­rung oder was auch immer in den Kel­ler, worüber die Impfun­gen ver­nach­läs­sigt wurden.



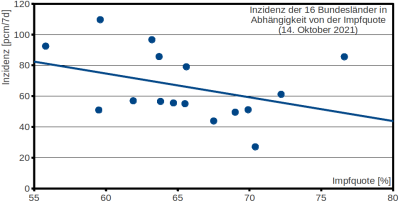
Je höher die Impfquote, desto niedriger die Inzidenz (png)

Theorie hin oder her, der Zusammen­hang ist nicht nur ver­schwun­den, er hat sich ins erwar­tungs­gemäße Gegen­teil verkehrt. Aus dem Impf­para­dox wurde ein Impf­ortho­dox. Mit jedem Pro­zent Impf­quote sinkt die Sieben­tage­inzi­denz um 1,5 pcm.

Jeder kennt aus seiner Kind­heit Abzähl­verse, um den näch­sten Kan­di­da­ten zu be­stim­men. Zum Bei­spiel „a ba bu und ab bist du“. Nor­ma­ler­weise sind sie etwas län­ger, doch bereits bei die­sen sie­ben Sil­ben ist es schwie­rig vor­her­zuse­hen, wel­che Posi­tion es tref­fen wird, um sich an sie zu stellen oder sie zu meiden. Die nach­ste­hende Abbil­dung zeigt links zweimal fünf abzu­zäh­lende Posi­tio­nen. Die letzte ist die rechts in der Reihe ste­hende oder die abzäh­len­de Per­son selbst. Im linken Teil­bild wird immer wie­der vorne begon­nen, und es trifft zum Schluß die fünfte Posi­tion. Diese Methode ist unschön, wenn mehr Per­so­nen n in der Reihe stehen als der Abzähl­vers Sil­ben k hat. Dann fällt dumm auf, daß es stets zunächst die hin­teren Posi­tio­nen k bis n trifft. Des­halb wird bes­ser wie im zwei­ten Teil­bild nach dem Aus­schei­den einer Per­son an der rechts dane­ben fort­gefah­ren. Ich meine, daß es in mei­ner Kind­heit so war. Alles andere hätte mir dumm auf­fal­len müs­sen.

1 2 3 4 5   1 2 3 4 5   00000000011111111112222222222333333333344
a b b u a   a b b u a   12345678901234567890123456789012345678901
b d | | |   b d a b b   ||X||X||X||X||X||X||X||X||X||X||X||X||X||
a   b b u   u   a b d   X| |X || X| |X || X| |X || X| |X || X| |X
a   b d |   a   b b      | |  X|  | X  ||  X |  |X  | |  X|  | X
a   b   b   u   a b      | |   X  |    |X    |  |   X |   |  X
u   a   b   d   a b      | |      X    |     |  X     |   |
d   |   |       b u      X |           |     X        |   |
    a   b       a b        X           |              |   X
    b   u       d Λ                    |              |
    a   b         |                    X              |
    d   |<-----letzter            Josephus        letzter

Während Kinder im all­gemei­nen wenige Posi­tio­nen mit lan­gen Ver­sen abzäh­len, sind es im rech­ten Teil­bild viele Posi­tio­nen n=41 und wenige Sil­ben k=3. Flavius Jose­phus wollte angeb­lich mit 40 wei­teren Gefan­genen Selbst­mord bege­hen. Nach­dem das Los bereits 39 das Leben kostete, war Jose­phus selbst an der Reihe. Da ergaben sich die rest­lichen beiden den Römern. Das führte zu der Frage: An welcher Posi­tion stand Jose­phus, wenn 41 Leute sich im Kreis auf­stellen und begin­nend mit der Posi­tion 3 jeder dritte erschlagen wird? Das vor­ste­hende Bild liefert die Antwort.

Das allgemeine Jose­phus-​Pro­blem  besteht darin, die Posi­tion p des letzten für alle n und k zu ermit­teln. Eine geschlos­sene Lösung ist wohl über k=3 hinaus nicht bekannt. Doch für k=2 ist es recht einfach:

0000000001111111111222222222233333333334444444444555555555566666
1234567890123456789012345678901234567890123456789012345678901234
|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X|X
| X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X
|   X   |   X   |   X   |   X   |   X   |   X   |   X   |   X
|       X       |       X       |       X       |       X
|               X               |               X
|<--letzter                     X

Die vorstehende Abbil­dung zeigt, daß für Zweier­poten­zen n=2ᵐ in jedem der m Um­läu­fe die An­zahl hal­biert wird und die Posi­tion 1 übrig­bleibt. Ist nun n=2ᵐ+l mit l<2ᵐ, dann kom­men zu­nächst die l Po­si­tio­nen 2, 4, 6, …, 2l<n ums Leben. Danach stehen noch 2ᵐ Mann. Nun ist der an Posi­tion p=2l+2 an der Reihe, und sein Vorgänger bei p=2l+1 bleibt letzt­lich übrig. Wer diese Über­le­gung scheut, aber pro­gram­mie­ren kann, der er­stellt sich eine Ta­belle, erkennt das Prin­zip und hofft, daß es sich so fort­setzt.

 n        p        n          p         n            p
1   1    1 1      8 1000  0001  1     15  1111   1111 15
2  10   01 1      9 1001  0011  3     16 10000  00001  1
3  11   11 3     10 1010  0101  5     17 10001  00011  3
4 100  001 1     11 1011  0111  7     18 10010  00101  5
5 101  011 3     12 1100  1001  9     19 10011  00111  7
6 110  101 5     13 1101  1011 11     20 10101  01011  9
7 111  111 7     14 1110  1101 13     21 10110  01101 11

Es gibt eine nette Spie­lerei, zur An­zahl n die Posi­tion p des Über­leben­den zu bestim­men: Aus der Binär­dar­stel­lung der Zahl n wird die füh­ren­de 1 ge­stri­chen und hin­ten ange­fügt. So er­gibt sich eine Binär­dar­stel­lung der Posi­tion p. Der Grund ist ein­fach: Durch das Ent­fer­nen der füh­ren­den 1 geht n in n−2ᵐ=l über. Das Anfü­gen ei­ner 1 am Ende macht aus l dann 2l+1=p.

[1] Wolfram Mathworld. Josephus Problem.

[2] The On-Line Encyclopedia of Integer Sequences. A032434, A006257, A054995.

41 | Sieb von Josephus

In den letzten Tagen hatte ich damit gerech­net, daß auf den letz­ten Metern, ins­beson­dere den 31 Fuß vor der Urne wie­der die Angst vor der Ver­ände­rung siegt und die CDU knapp vor der SPD lan­det. Dann wäre Scholz stolz gewe­sen, die SPD aus dem Kel­ler geholt zu ha­ben, obgleich es aus der Oppo­si­tion heraus hätte über­zeu­gen­der aus­fal­len können.

Da Laschet von weit oben auf dem zwei­ten Platz lan­dete, sollte er eigent­lich zurück­tre­ten und nicht den Schrö­der machen. Wenn die CDU kon­sequen­ter ist als die SPD vor vier Jahren, dann schickt sie Laschet in die Wüste und rege­ne­riert sich in der Oppo­sition.

Leider ist den Grü­nen und vor allem der FDP alles zuzu­trauen. Sie könnten sich für den schwä­cheren Häupt­ling ent­schei­den, um mehr Posten zu ergat­tern. Viel­leicht ist das lang­fri­stig mit oder ohne Regie­rungs­wech­sel oder Neu­wahlen die beste Vari­ante für die SPD.

4 von 7 | Schwarz-Rot | Heute Zwerg, morgen Riese | Koali­tion der Mitte | Gemein­same Nenner | Pünkt­chen­partei

Die Liste aller Wikipedia-​Artikel mit Corona im Titel ist lang. Jedem werden spontan Auto­marken, Fuß­ball­spieler, Bier, Sonnen­finster­nisse oder Herz­kranz­gefäße in den Sinn kom­men. Über­wälti­gend ist die Zahl der Kronen, die es gab und rück­stän­diger­weise immer noch getra­gen werden. Auch Penis­bilder sind dabei. Nicht unter den ersten 300 das Corona-​Theorem, das ich nach einem halben Jahr­hun­dert kaum noch verstehe, obgleich ich im Rahmen eines Semi­nares die Ehre hatte, einen Beweis des Prä-​Corona-​Theo­rems vor­zu­tra­gen. Nun lautet mein Post-​Corona-​Theo­rem: In den zivi­lisier­ten Län­dern ist Corona dank Impfun­gen auf dem ab­stei­gen­den Ast. Der Wider­stand ist gebro­chen, die Hör­ner sind auf dem Rück­zug.

Weil David Wells [1] die 39 kleinste uninter­essante Zahl nannte, wurde nach deren Beson­der­hei­ten gesucht. Natür­lich wur­den sie gefun­den, und ich zog 38 in Betracht, danach 43 und 45, über­sah aber die 29, über die es wahr­lich neben den 29 Ta­gen des Februar in Schalt­jahren nicht viel zu sagen gibt.

Die Wikipedia vermerkt 29=2²+3²+4² als die klein­ste Prim­zahl unter den Summen dreier Quadrate in Folge. Das ist weit her­geholt, denn die Prima­lität ist in diesem Zusam­men­hang bedeu­tungs­los und soll nur 14=1²+2²+3² aus­schlie­ßen. Zwar ist die 29 durch diese Bezie­hung als drei­stufi­ger Pyra­miden­stumpf dar­stell­bar, wird dadurch aber nicht zu einer figu­rier­ten Zahl.

Ganz nett ist der Umstand, daß 29 die kleinste Zahl ist, die nicht durch ein­malige Verwen­dung der Zah­len 1 bis 4 allein mit Hilfe der vier Grund­rechen­arten dar­stell­bar ist. Für Zahlen bis 28 findet man Lösungen mehr oder minder leicht.

22 = 2·(3·4-1)  25 = (4+1)·(2+3)   28 = 4·(2·3+1)
23 = 2·3·4-1    26 = 2·(3·4+1)     29 geht nicht
24 = 1·2·3·4    27 = 3·(2·4+1)     30 = 2·3·(1+4)

Hätte 29 eine Darstellung, bliebe wegen der Prima­lität nur 29=x+y und oBdA x≥15, wofür wegen 3·4=12 drei der vier Zahlen aufzu­wenden sind. Somit stünde nur eine Zahl für y≤4 zur Verfü­gung. Das bedeu­tete x≥25, was wegen 2·3·4=24 für nur drei Zahlen zuviel ist.

Meine einzige Erinne­rung an 29 war ihr Vor­kom­men unter den Nähe­rungen für die Wurzel aus 2: Aus einer Näherung p/q kann eine bessere (p+2q)/(p+q) gewon­nen werden. Mit p=q=1 begin­nend sind die ersten Schritte:

 1/1  --> ( 1+2·1 )/( 1+1 ) =  3/2  = 1,5
 3/2  --> ( 3+2·2 )/( 3+2 ) =  7/5  = 1,4
 7/5  --> ( 7+2·5 )/( 7+5 ) = 17/12 = 1,4167
17/12 --> (17+2·12)/(17+12) = 41/29 = 1,4138
41/29 --> (41+2·29)/(41+29) = 99/70 = 1,4143

Interessant sind eigentlich nur 7/5 und 99/70, die bereits in der Antike genutzt wur­den, weil sie im Gegen­satz zu 41/29 keine Prim­fak­toren ober­halb von 11 ent­hal­ten.

[1] David Wells: The Penguin Dictionary of Interesting and Curious Numbers.

28 | 30 | 38 | 39 | 43 | 45 | Schalttag | Uninter­essante Zahlen

Die Zahl 128 ist die siebte Zweierpotenz, also 10000000 als Binär­zahl. [1] Sie kommt wie 8, 256, 1024, 8192 in der Daten­verar­bei­tung vor, zum Bei­spiel als Unix-​Block­länge und vor allem als Anzahl der Zeichen im ersten 7-Bit-​ASCII-​Code. [2]

Wer nach 128 googelt, wird kaum mehr finden, aktuell aber das Bemühen von Erdo­wahn, die Nen­nung der Zahl zu unter­binden, manche sagen zu ver­bieten, weil sie auf 128 Mil­liar­den ver­schwun­dene Lira, etwa 12,5 Mil­liar­den Euro anspielt. Es soll deshalb schon die Frage gestellt worden sein, wo die andere Hälfte der 256 geblie­ben sei. So lernen die Türken Zweier­potenzen.

Aber wir müssen uns gar nicht lustig machen, denn in Deutsch­land werden allent­halben 14, 18 und 88 auf Nummern­schil­dern unter­sagt. Ginge es nach den Nazi-​Jägern, könn­ten es noch viel mehr sein. Auch die Ver­öffent­lichung einer Zahl zur DVD-Ver­schlüs­selung war ver­boten. Natur­gemäß blieb sie nicht lange geheim. [3]

Solange dieser Beitrag zur Zahl 128 von Google nicht gefun­den ist, wird die schöne Bezie­hung zwi­schen der Binär­zahl 10000000 und dem heu­tigen Nicht-​Binär-​Tag kaum einer bemer­ken: Er wurde auf den fran­zösi­schen Natio­nalfei­ertag (14. Juli) gelegt, damit er sich genau in der Mitte zwi­schen dem Frauen­tag (8. März) und dem Männer­tag (19. No­vem­ber) befin­det. Damit beträgt der Abstand zu beiden Polen genau 128 Tage, als Binär­zahl 10000000. Offen­sicht­lich konnte die LGBTQIA-​Gemeinde sich nicht von der über­kom­menen Welt zwi­schen dunk­lem Yin (4. Geschlecht: weib­lich) und hellem Yang (9. Geschlecht: männ­lich) trennen. [4] Beim Sesqui­gender­tag muß das besser werden. Da muß auch nicht-​binär-​korea­nisch dabei sein. [5]

[1] Manche meinen wie die Wikipedia, das Binär­system hieße besser Dual­system. Dann müßten wir auch von Dual­zahlen statt Binär­zahlen sprechen. Auch von Dual­darstel­lung statt Binär­darstel­lung. Da endet zumeist der Purismus, feiert aber bei den Se- bzw. Hexa­dezimal­zahlen und den Sexa- bzw. Hexa­gesimal­zahlen fröh­liche Urständ, statt lieber der Mensch­heit den Unter­schied zwi­schen einem Duett und einem Duo zu erklären.

[2] Der enthielt natürlich keine Umlaute und andere Zeichen, weshalb es länder­spezi­fische Abwei­chun­gen gab. So ersetz­ten im deuts­chen ASCII-​Code ÄÖÄäöüß die US-Zei­chen [\]{|}~ mit ent­spre­chen­den Pro­blemen, die sich bis auf den heu­tigen Tag nur verla­gert haben.

[3] Natürlich gibt es geheimzuhaltende Zahlen, die nur wenigen oder gar keinem bekannt sind. Aber eine Reser­vie­rung von auch noch so großen Zahlen sollte es nicht geben. Keine Patente und kein Copy­right, auch nicht für 4711.

[4] Besser gefallen hätte mir statt 4 die Nummer 6 für cis-Frauen, eine in 69 auf dem Kopf ste­hen­der Mann 9.

[5] Britischer Influencer outet sich als "nicht-​binär-​korea­nisch". Kurier, 24.06.2021.

2 | 6 | 9 | 69 | 14 | 18 | 88 | Planeten | Symmetrie | Titanic | Trigender