Ulam-Spirale
wuerg, 09.10.2005 15:57
So mancher hat vielleicht schon aus Langeweile die Zahlen auf kariertem Papier in der Form einer rechtwinkligen Spirale
In der Hauptdiagonalen stehen die grünen Rechteckzahlen Rₙ=n(n+1), abwechselnd vom Zentrum nach rechts oben und links unten. Nicht ganz so schön ordnen sich die roten Quadratzahlen an. Die geraden gehen auf der Nebendiagonalen nach links, die ungeraden um eine Position versetzt nach rechts unten etwas versetzt von der 1 aus. Sowohl die Rechteck- als auch die Quadratzahlen stehen an den Ecken der Spirale. [2]
Jede von einer Zahl a nach außen weisende Diagonale besteht aus Zahlen 2n(2n+b)+a, ist also eine aufsteigende quadratische Progression. Zum Beispiel 4n²+12n+7 für die nach rechts unten weisende Folge 7,23,47,79,… Die recht langen Strecken von diagonal liegenden Primzahlen sind also nichts anderes als eine Veranschaulichung der Tatsache, daß in quadratischen Progressionen Primzahlen offensichtlich leichter aufeinander folgen als in linearen, wenn auch selten so hartnäckig wie im Eulerschen Primpolynom n(n−1)+41.
[1] Ursprünglich hatte ich die die Ulam-Spirale in einer ordentlichen Tabelle dargestellt und die Primzahlen zur besseren Erkennung mit gelben Hintergrund versehen, doch zunächst fiel unter blogger.de bgcolor in Tabellenfeldern aus, später wurden Tabellen gänzlich unterdrückt.
[2] Dieses Hin und Her macht deutlich, daß eine Spirale nicht die ideale Art und Weise ist, die Zahlen anzuordnen, um Reihungen zu erkennen.
[3] Wolfram Mathworld. Prime Spiral.
[4] T. Goddard: Ulam Spiral
41 | Primzahlkreuz
15--14--13--12
|
4---3---2 11
| | |
5 0---1 10
| |
6---7---9---9
aufgemalt. Auch Stanislav Ulam fand neben dem Bau der Wasserstoffbombe Zeit dazu. Und vielleicht war er wirklich der erste, der eine Klumpung der Primzahlen entlang der Diagonalen bemerkte, die ich im nachfolgenden Diagramm blau dargestellt habe. [1]99 98 97 96 95 94 93 92 91 90 64 63 62 61 60 59 58 57 56 89 65 36 35 34 33 32 31 30 55 88 66 37 16 15 14 13 12 29 54 87 67 38 17 4 3 2 11 28 53 86 68 39 18 5 0 1 10 27 52 85 69 40 19 6 7 8 9 26 51 84 70 41 20 21 22 23 24 25 50 83 71 42 43 44 45 46 47 48 49 82 72 73 74 75 76 77 78 79 80 81Ulam-Spirale, ungerade Primzahlen blau, Quadratzahlen rot, Rechteckzahlen grün (htm, png)
In der Hauptdiagonalen stehen die grünen Rechteckzahlen Rₙ=n(n+1), abwechselnd vom Zentrum nach rechts oben und links unten. Nicht ganz so schön ordnen sich die roten Quadratzahlen an. Die geraden gehen auf der Nebendiagonalen nach links, die ungeraden um eine Position versetzt nach rechts unten etwas versetzt von der 1 aus. Sowohl die Rechteck- als auch die Quadratzahlen stehen an den Ecken der Spirale. [2]
Jede von einer Zahl a nach außen weisende Diagonale besteht aus Zahlen 2n(2n+b)+a, ist also eine aufsteigende quadratische Progression. Zum Beispiel 4n²+12n+7 für die nach rechts unten weisende Folge 7,23,47,79,… Die recht langen Strecken von diagonal liegenden Primzahlen sind also nichts anderes als eine Veranschaulichung der Tatsache, daß in quadratischen Progressionen Primzahlen offensichtlich leichter aufeinander folgen als in linearen, wenn auch selten so hartnäckig wie im Eulerschen Primpolynom n(n−1)+41.
[1] Ursprünglich hatte ich die die Ulam-Spirale in einer ordentlichen Tabelle dargestellt und die Primzahlen zur besseren Erkennung mit gelben Hintergrund versehen, doch zunächst fiel unter blogger.de bgcolor in Tabellenfeldern aus, später wurden Tabellen gänzlich unterdrückt.
[2] Dieses Hin und Her macht deutlich, daß eine Spirale nicht die ideale Art und Weise ist, die Zahlen anzuordnen, um Reihungen zu erkennen.
[3] Wolfram Mathworld. Prime Spiral.
[4] T. Goddard: Ulam Spiral
41 | Primzahlkreuz
... comment
pappnase,
09.10.2005 16:14
warum ist bei der langeweilespirale keine acht dabei?
... link
wuerg,
09.10.2005 16:20
Ich sehe die 8 ganz deutlich. Schließlich wurde sie von dem Holländer van der Acht bereits im Jahre 1729 zwischen der 7 und der 9 entdeckt.
... link
wuerg,
09.10.2005 16:35
Zwischenzeitlich habe ich es auch gesehen. Ich habe in meine mühselig erstelle HTML-Tabelle geguckt und Sie in die bescheidene Text-Spirale. Dort habe ich tatsächlich 9 statt 8 geschrieben. Ich lasse es so. Zum einen muß Ihre Entdeckung für weitere Heerscharen von Lesern nachvollziehbar sein. Zum anderen ist es ein guter Aufmerksamkeitstest.
... link
... comment
wuerg,
10.10.2005 12:26
Auch ich kann es nicht mehr vermeiden. Es müssen Bilder in den Text, auch wenn es nur einfache Tabellen sind. Und so hätte meine Tabelle ausgesehen, wenn HTML vorschriftsmäßig interpretiert würde:
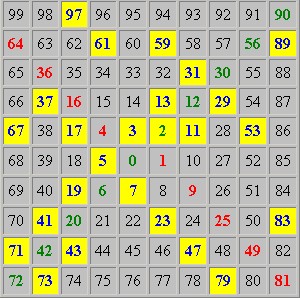
Vielleicht sollte ich einfach alles mit der Hand schreiben und nur noch Bilder veröffentlichen?

Vielleicht sollte ich einfach alles mit der Hand schreiben und nur noch Bilder veröffentlichen?
... link
axelk,
13.10.2005 21:54
html wird schon 'vorschriftsmäßig' interpretiert. Sie kommen hier nur mit ihrem stylesheet ins gehege ;)
body, td {
background-color: #ffffff;
[..]
.. deswegen sind die zellen weiss.... link
wuerg,
14.10.2005 00:57
Vielen Dank für den Hinweis. Ich muß zugeben, mir den bei mir ankommenden Quellcode noch gar nicht angesehen zu haben, und war deshalb der irrigen Erstannahme, gewisse Attribute würden herausgefiltert. Nun sehe ich in main.css auch den Grund für ein anderes Übel, nämlich „align=center“ für Tabellenfelder.
Auch wenn ich es nicht für gerechtfertigt halte, umfangreiche Style-Vereinbarungen auf so niedriger Ebene wie Tabellenfelder zu treffen, werde ich nichts ändern. Sie werden sicherlich an meinem Layout gesehen haben, daß ich bis auf die paar Zeilen unter „Favorite Items“ alles im Anfangszustand belassen habe.
Auch wenn ich es nicht für gerechtfertigt halte, umfangreiche Style-Vereinbarungen auf so niedriger Ebene wie Tabellenfelder zu treffen, werde ich nichts ändern. Sie werden sicherlich an meinem Layout gesehen haben, daß ich bis auf die paar Zeilen unter „Favorite Items“ alles im Anfangszustand belassen habe.
... link
wuerg,
14.10.2005 17:51
Jetzt weiß auch ich, warum ausgerechnet für td unangenehme Stylevereinbarungen getroffen werden: Um den Kalender mit sparsamen Statements anzuzeigen.
Mit Entsetzen sehe ich auch die am Ende meiner Tabelle hinzugefügten /td, /b und /font, die ich mir alle gespart habe. Es wird also doch mehr an der Eingabe verändert als nur der Zeilenumbruch.
Mit Entsetzen sehe ich auch die am Ende meiner Tabelle hinzugefügten /td, /b und /font, die ich mir alle gespart habe. Es wird also doch mehr an der Eingabe verändert als nur der Zeilenumbruch.
... link
... comment
wuerg,
13.10.2005 00:08
Wenn man gelangweilt dasitzt und die Zahlen quadratisch anordnet, dann würden die meisten wohl wie Ulam um ein kleines Anfangskästchen eine Umrandung malen, darum wieder eine, und so fort. Das ist die moderne zentrierte Denkweise. Die Griechen dachten sich die Quadratzahlen etwas konsequenter von einer Ecke her, zu der schrittweise Winkel hinzugenommen werden. Diese Vorstellung führt auf eine verbesserte quadratische Darstellung der Zahlen, die man noch Ulam nennen könnte, doch nicht mehr Spirale.
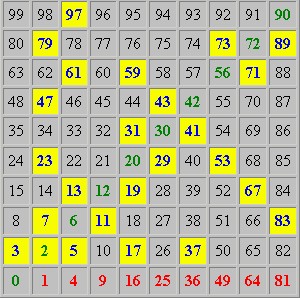
Wieder sind lange Ketten wie 5,11,19,29,41 und 59,43,41,53,67,83 zu erkennen. Die nach rechts-oben weisenden Diagonalen sind allesamt aufsteigend und folgen mit n(n+b)+a einer schlichteren Formel als die der Ulam-Spirale. Geht man noch einen Schritt weiter, klopft die rechte obere Ecke platt und dreht alles um 135 Grad nach rechts, so kommt man auf die Darstellung
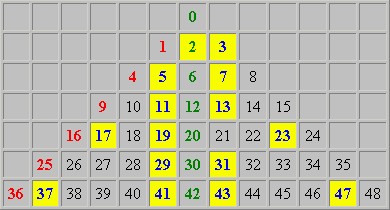
in der die Kette 5,11,19,29,41 einfach als Spalte erscheint, weil alle nach rechts-oben weisenden Diagonalen nun einfach senkrecht nach unten verlaufen. Und wenn man den linken Teil der Pyramide entfernt, sie dafür aber nach rechts ausbaut, erhält man
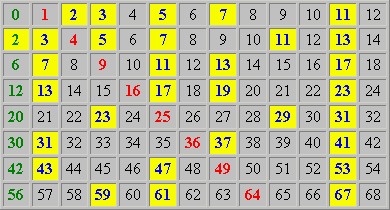
in der die oben mit a beginnende Spalte einfach die Zahlen n(n−1)+a enthält. Schon unter diesen einfachen Folgen kommen überraschend lange Primzahlketten vor. Die mit 11 beginnende Spalte ist vollständig gelb, was sich im nicht dargestellten Bereich fortsetzt, jedoch nicht für immer. [1,2]
[1] Irgendwann ist jede Serie zuende, denn für jede Spalte a≥2 sind die Zahlen in den Zeilen n=k⋅a und n=k⋅a+1 für k>0 echt durch a teilbar, also nicht prim. In der Spalte für a=0 gibt es nur gerade Zahlen, also nur die eine Primzahl 2. Und für a=1 ist nach der 3 jede dritte Zahl echt durch 3 teilbar.
[2] Von oben beginnend gibt es für a=2,3,5,1,17,41 Primzahlserien der Länge a−1, die erst von der Diagonalen (n=a) beendet werden. Letztere ist das berühmte Eulersche Primpolynom n(n−1)+41. Es gibt längere Serien, doch nicht von oben. [3] Und sehr beeindruckend wäre, wenn man die längste kennte und es nicht a=41 wäre.
[3] Wolfram Mathworld. Prime-Generating Polynomial.

Wieder sind lange Ketten wie 5,11,19,29,41 und 59,43,41,53,67,83 zu erkennen. Die nach rechts-oben weisenden Diagonalen sind allesamt aufsteigend und folgen mit n(n+b)+a einer schlichteren Formel als die der Ulam-Spirale. Geht man noch einen Schritt weiter, klopft die rechte obere Ecke platt und dreht alles um 135 Grad nach rechts, so kommt man auf die Darstellung

in der die Kette 5,11,19,29,41 einfach als Spalte erscheint, weil alle nach rechts-oben weisenden Diagonalen nun einfach senkrecht nach unten verlaufen. Und wenn man den linken Teil der Pyramide entfernt, sie dafür aber nach rechts ausbaut, erhält man

in der die oben mit a beginnende Spalte einfach die Zahlen n(n−1)+a enthält. Schon unter diesen einfachen Folgen kommen überraschend lange Primzahlketten vor. Die mit 11 beginnende Spalte ist vollständig gelb, was sich im nicht dargestellten Bereich fortsetzt, jedoch nicht für immer. [1,2]
[1] Irgendwann ist jede Serie zuende, denn für jede Spalte a≥2 sind die Zahlen in den Zeilen n=k⋅a und n=k⋅a+1 für k>0 echt durch a teilbar, also nicht prim. In der Spalte für a=0 gibt es nur gerade Zahlen, also nur die eine Primzahl 2. Und für a=1 ist nach der 3 jede dritte Zahl echt durch 3 teilbar.
[2] Von oben beginnend gibt es für a=2,3,5,1,17,41 Primzahlserien der Länge a−1, die erst von der Diagonalen (n=a) beendet werden. Letztere ist das berühmte Eulersche Primpolynom n(n−1)+41. Es gibt längere Serien, doch nicht von oben. [3] Und sehr beeindruckend wäre, wenn man die längste kennte und es nicht a=41 wäre.
[3] Wolfram Mathworld. Prime-Generating Polynomial.
... link
gemir,
03.07.2015 01:35
Wie kommen Sie auf die Darstellung 2n(2n+b)+a? Eine etwas ausführlichere Erklärung, warum es so ist, wäre sehr wünschenswert. Danke.
... link
wuerg,
11.07.2015 18:06
Sind a₀, a₁, a₂, … die Zahlen auf einer nach außen gerichteten Diagonalen und werden b₀ Schritte für die erste Runde von a₀ nach a₁ benötigt, so sind es für die nächste Runde b₁=b₀+8, für die übernächste b₂=b₀+16 usw. Für die Runde von aₖ nach aₖ₊₁ also bₖ=b₀+8k Schritte. Damit ist
an = a0 + b0 + b1 + b2 + … + bn−1
= a0 + b0 + (b0+8) + (b0+8·2) + … + (b0+8⋅(n−1))
= a0 + nb0 + 8⋅(1+2+…+(n−1))
= a0 + nb0 + 8⋅(n(n−1)/2)
= a0 + 2n⋅(2n+b0/2−2)
= 2n⋅(2n+b) + a
worin a=a₀ und b=b₀/2−2 gesetzt wurde. Auch b ist eine ganze Zahl, weil b₀ gerade ist. Das sieht man sofort, wenn man sich das Quadrat wie ein Schachbrett mit schwarzen und weißen Feldern vorstellt. Diagonal ändert sich die Farbe nicht, in jedem Schritt aber schon. Die 8 rührt daher, daß in jeder neuen Runde vier Kanten mit jeweils zwei weiteren Schritten zu durchlaufen sind.
an = a0 + b0 + b1 + b2 + … + bn−1
= a0 + b0 + (b0+8) + (b0+8·2) + … + (b0+8⋅(n−1))
= a0 + nb0 + 8⋅(1+2+…+(n−1))
= a0 + nb0 + 8⋅(n(n−1)/2)
= a0 + 2n⋅(2n+b0/2−2)
= 2n⋅(2n+b) + a
worin a=a₀ und b=b₀/2−2 gesetzt wurde. Auch b ist eine ganze Zahl, weil b₀ gerade ist. Das sieht man sofort, wenn man sich das Quadrat wie ein Schachbrett mit schwarzen und weißen Feldern vorstellt. Diagonal ändert sich die Farbe nicht, in jedem Schritt aber schon. Die 8 rührt daher, daß in jeder neuen Runde vier Kanten mit jeweils zwei weiteren Schritten zu durchlaufen sind.
... link
... comment
kid37,
17.11.2005 22:41
Ich bin immer wieder völlig eingenommen von den Mysterien Ihrer Zahlenkunde.
... link
... comment
