Zahlwort

Bei XYZZY handelt es sich um ein bekanntes Zauber­wort. [1] Wer seinen Computer voll­ständig nach XYZZY durch­sucht, kann es finden. Zumindest unter alten Windows-​Versionen, denn XYZZY bewog Mine­sweeper, im oberen linken Pixel anzu­zeigen, ob der Cursor sich gerade über einer Bombe befindet. Wie um die Zahl 42 kann man auch über XYZZY rätseln. Evtl. ist es ein Merk­spruch für das Kreuz­produkt c=axb dreidimen­sionaler Vektoren:

c_x = a_y·b_z - a_z·b_y
c_y = a_z·b_x - a_x·b_z
c_z = a_x·b_y - a_y·b_x

Manche meinen, XYZZY sei der erste „cheat“. Doch dem ist nicht so, denn XYZZY ist kein geheimer Befehl, der Program­mierern einen zügigen Höhlen­durchlauf oder ungeduldigen Spieleabhakern einen schnellen Erfolg ermöglicht, sondern ein zu entdeckender Befehl.


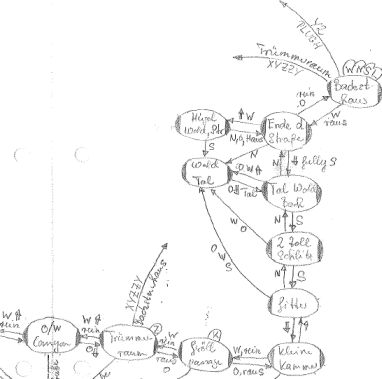
Startbereich aus der Sicht eines deutschen Höhlenforschers

Das vorstehende Bild zeigt einen Plan des deutschen Höhlen­forschers aus dem Jahre 1981 mit der durch XYZZY vermit­telten Abkür­zung zwischen Backsteinhaus und Trümmer­raum. Woanders wird das zum geflügelten Wort gewordene „Nothing happens“ gemeldet.

[1] You are in a twisty maze of passages, all alike - XYZZY. Ein gewisser Reb hat sich die Seite xyzzy.com gesichert, die auf weiter­führende Informa­tionen zum 350-Punkte-​Aben­teuer verweist.

2. Wandertag | Übersicht | abenteuer (pdf, 163 KB)

Nach Berichten über meinen ersten Computer LOCI-2 und das einzig verstandene Betriebssystem CP/M nun das liebste aller Textverarbeitungs­programme: Wordstar. Was davor und danach an Editoren und Text­verarbeitungs­systemen kam, nahm ich nur noch soweit zur Kenntnis, wie ich es unbedingt benötigte. Über sie mag ich dicke Handbücher besessen und teilweise auch gelesen haben, gelegentlich legte ich mir sogar ein Buch über sie zu, doch mehrere gut studierte Bücher habe ich nur über Wordstar. Voran das wohl beste "Einführung in Wordstar" von Arthur Naiman, der sein Buch aber nicht mit Wordstar geschrieben haben soll, weil es wegen seiner dauernden Disketten­zugriffe zu langsam sei.

Mit Wordstar war es mir erstmal möglich, sowohl schlichten Text (N-Modus) zu schreiben, wie er für Programme unbedingt erforderlich ist, als auch sogenannte Dokumente(D-Modus), die zusätzlich zahlreiche Layout-Funktionen enthielten. Davor lag das Zeitalter der Schreibmaschine, da man Layout mit der Hand oder dem Setzkasten erstellte und notfalls alles neu schrieb. Mit der Daten­verarbeitung und vor allem der Programmierung aber waren Editoren erforderlich, deren Ergebnis maschinen­lesbar sein mußte.

Mein erster Editor diente dem Schreiben der Programme für den LOCI-2. Das war ich selbst, indem ich mit einem schraubenzieherähnlichen Gerät in eine Lochkarte mit 480 perforierten Positionen Löcher stanzte. Ihm folgte eine Lochkarte mit Magnetstreifen, auf dem wenige zuvor eingegebene Daten speicherbar waren. Und bevor ich Jahre später als Student an ein Terminal mit einem einfachen Editor gelassen wurden, war alles auf Lochkarten zu stanzen. Der höchste Korrektur­komfort bestand darin, links die alte Karte lesen und rechts korrigiert neu stanzen zu lassen.

Ich will nicht jammern, denn auch vor Wordstar gab es mächtige Editoren. Nur mußte man sich den alten Text umständlich anzeigen lassen, am besten gut im Kopf oder gedruckt vorliegen haben. Dokumente im heutigen Sinne, also Texte mit viel Schnick­schnack, gab es auf Rechnern kaum. Sie waren den Schriftsetzern und Druckereien vorbehalten. Mit Wordstar wurde das in weiten Kreisen anders, auch zuhause. Man konnte doppelt, breit, unterstrichen und mit einem mehrfarbigen Farbband auch bunt drucken. Es gab Ränder, Kopf- und Fußzeilen, Fließtext, Randausgleich, nicht trennbare Leerzeichen, feste Zeilenumbrüche, was heute selbstverständlich ist und dennoch oft mißachtet wird. Wordstar begründete das eigentlich nie erreichte WYSIWYG und Mailmerge den Serienbrief von daheim.

Doch auch Wordstar überlebte nicht. Sein Tod war mit dem von CP/M besiegelt. Zahlreiche Schreibprogramme wie TECO, PE, Signum-2, Locoscript, med, SEU, EVE, WPS, Wordperfect kamen und gingen, vi blieb wegen seiner plumpen Mächtigkeit, und heute dominiert Word die Welt. Mit dem ganzen MS-Office-Kram konnte ich mich nie mehr anfreunden und benutze ihn nur, wenn er gefordert ist, Schnick­schnack demonstriert werden soll oder im Einzelfall auch ganz nützlich ist, um zum Beispiel mit Excel schnell eine Kurve zu zeichnen oder mit Word die übelsten Rechtschreib­fehler zu finden. Ansonsten hat sich die in Wordstar vereinte Welt (D und N) wieder getrennt: Schlichten Text, HTML und elektronische Post schreibe ich mit Notepad.

Über meinen ersten Computer wollte ich schon immer etwas schreiben. Es ist der sagen­umwobene LOCI‑2 der Firma Wang, der natürlich nicht mir gehörte, weil er etwa 20.000 Mark kostete, obwohl er gut auf einen kleinen Tisch paßte. Zu dieser Zeit gab es zwar schon Groß­rechner, doch an die hatte mich noch keiner gelassen. Der volle Name war „Loga­rithmic Compu­ting Instru­ment“ und benennt seine einzig­artige Fähig­keit, den Loga­rithmus (ln) und dessen Umkehr­funk­tion (exp) zu berech­nen. Natür­lich konnte er auch addieren und subtra­hieren. Alles andere aber wurde indirekt erledigt, selbst die Multi­plikation a⋅b durch exp(lna+lnb).

Wenn man bei diesem LOCI‑2 von einer CPU sprechen will, so war sie auf mehrere große Platinen aufge­teilt und bestand neben vielen herkömm­lichen elek­troni­schen Bautei­len aus 1200 Tran­sistoren. Der Magnet­kern-​Haupt­speicher sah aus wie ein Lüfter und umfaßte 96 Byte, das sind 768 Bit organ­isiert in 16 Zahlen zu 48 Bit. Das sind 10 BCD-​Zif­fern sowie 8 Bit für das Vorzei­chen und die Posi­tion des Dezimal­punktes. Jedes Bit war einzeln als Ring zu sehen, durch den vier Drähte gingen.

Der Bild­schirm bestand aus 10 Dezimal-​Anzeige-​Röhren und einer für das Vor­zeichen. Sobald sie nicht mehr flacker­ten, war die Arbeit bendet oder eine weitere Eingabe erforder­lich, für die es bereits eine Tastatur gab. Das absolut beste an dem Rechner war aber sein Programm­speicher, eine Klappe mit 480 Kontakten, in die man eine normale Lochkarte einlegen konnte. Auf ihr waren 80 Befehle in 6 Bit Breite möglich.

Ich erinnere mich gerne an diesen Rechner, weil ich für ihn mein erstes Programm geschrieben habe, das von wirk­lichem Nutzen war und an die Grenzen der Mög­lich­keiten ging, nämlich drei Gleich­ungen mit drei Unbe­kannten zu lösen. Das mag heute als Pipifax erschei­nen, doch bedenke man bitte, daß 12 Para­meter einzu­lesen waren, wonach nur etwa 60 Befehle zur Lösung in nur noch vier freien Spei­cher­plätzen blieben. Die Lösung bestand natür­lich in einer rekursiven Vorge­hens­weise, die 12 Para­meter viermal zyklisch zu ver­schieben, um so befehls­sparend die Deter­minanten der vier 3×3‑Ma­tri­zen zu berechnen, die dann mit drei Divi­sionen zum Ergebnis führten.

Leider habe ich dieses Programm nicht mehr. Es war sehr nütz­lich, denn es waren stets drei Gleich­ungen mit drei Unbe­kannten zu lösen, wollte man aus drei Ver­suchs­färbungen die Zutaten für eine weitere berechnen, die mög­lichst genau den vorge­gebenen Farbton trifft. Aber dafür konnte der Rechner nicht ange­schafft worden sein, denn keiner konnte wissen, daß im Labor ein Lehr­ling herum­läuft, der auf ihm drei Gleich­ungen mit drei Unbe­kannten zu lösen in der Lage war. Und an eine mitge­kaufte Programm­biblio­thek kann ich mich nicht erinnern. Wahr­schein­lich sollte der Rechner einem profa­neren Zweck dienen, nämlich die mecha­nische Rechen­maschine ablösen und die eine oder andere Rechnung verein­fachen. Zum Beispiel:

Will man mit einer mecha­nischen Rechen­maschine oder dem Bill-​Gates-​Rechner von zehn Meß­werten nicht nur den Mittel­wert, sondern auch die Streu­ung berech­nen, so gehen die meisten immer noch so vor wie wir als Lehr­linge: Die zehn Werte werden addiert und durch 10 geteilt. Das liefert den Mittel­wert, der von allen Meß­werten abge­zogen wird. Diese zehn Diffe­renzen werden qua­driert und führen wie­derum addiert auf die Streu­ung. Bei diesem Ver­fahren muß leider jeder Meßwert zweimal einge­geben werden. Wer sich aus­kannte, wußte natür­lich, daß man Meß­werte und ihre Quadrate parallel addieren kann, um aus ihnen zum Schluß Mittel­wert und Streu­ung zu berechnen. Doch wo war auf einer Rechen­maschine der dazu nötige zweite Zwischen­speicher, und wo das Programm zum Abspulen der immer gleichen Opera­tionen? Antwort: Auf dem LOCI‑2!

[1] Rick Bensene: Wang LOCI-2. The Old Calculator Museum.

Bernd Pol | Anfang und Ende

In manchen Blogs kursierte die Frage nach dem Erstenmal, nämlich dem ersten Computer, dem ersten Betriebs­system, dem ersten Programm und dem ersten Spiel im Leben. Das nehme ich zum Anlaß, hier das erste und zugleich letzte von mir weit­gehend verstan­dene Betriebs­system CP/M zu loben. In den Vorgän­gern sah ich allen­falls eine Platt­form zum Schreiben und Ausführen von Pro­grammen, von den Nach­folgern verstand ich nur noch Bruch­stücke und Über­sichts­bilder.

Die für mein Leben heraus­ragende Bedeutung von CP/M erkenne ich auch am Besitz des wirklich gelesenen Buches [1] von Bernd Pol, der es beim ersten Band der Reihe beließ und sich anschlie­ßend der Dich­tung wid­mete. Wider sein Erwarten wurde dieses Buch mit einer Auflage von 30.000 das Stan­dard­werk in deut­scher Sprache.

Das Control Program for Micro­compu­ters (CP/M) war das erste Disk Operating System (DOS) und in den 80er Jahren in der Version 2.2 Stan­dard für Tisch­rechner mit Prozes­soren 8080 und Z80. Mit dem Schnei­der Joyce gelangte es auch unter das deut­sche Volk. Ich selbst lernte CP/M auf einem Tand­berg-​Rechner TDV 2324 mit zwei 8‑Zoll-​Dis­ketten-​Lauf­werken kennen, die bereits „double sided double density“ waren und 1 Mega­byte faßten. Diese Größen­ordnung wurde auf den 5‑1/4‑Zoll-​Dis­ketten der späteren IBM‑PC erst nach mehr­facher Ver­doppe­lung ihrer Kapa­zität wieder erreicht. Später durfte ich CP/M auf dem legen­dären Kontron PSI‑80 benutzen und hatte auch das nötige Klein­geld für einen Schneider Joyce.

Das Tandberg Operating System (TOS) und das Kontron Operat­ing System (KOS) dienten seiner­zeit zumeist nur dem Laden von CP/M. Es war Markt­führer im Bereich der Klein­rechner wie heute Micro­soft Windows und ist dennoch prak­tisch ausge­storben. Kurze Zeit hoffte ich, das Nach­folge­system MP/M für mehrere Benutzer würde sich auf dem über­legenen 16‑Bit-​Prozessor Z8000 durch­setzen. Doch leider ging die Evolu­tion den technisch stei­nigen Weg entlang des bekannten wirt­schaft­lichen Erfolges über 8086-​Prozes­soren und PC‑DOS zu dem was heute die Welt beherrscht. Darin lebt CP/M weiter, denn nicht wenig wurde von ihm abge­kupfert, wie CP/M auch nicht ohne Vor­bilder auskam.

Zurück zum Buch von Bernd Pol, besser zu meinem Exemplar. Ich habe mir die offen­sicht­lich oft aufge­schla­genen, die drecki­geren, die von meiner Tochter bekrit­zelten und die von mir korri­gierten Seiten ange­sehen:

Der Warmstart in Kapitel 3 (Wie CP/M Disketten verwaltet), wo beschrieben wird, was nach Eingabe von Control-C geschehen sollte. Meisten war es auch so, während heute gerne vergeblich auf eine Reaktion gewartet wird.

Diskettenmerkmale ermitteln in Kapitel 8 (STAT-Funktionen), wo die Glie­derung einer CP/M‐Dis­kette oder -Fest­platte in Spuren, Sektoren, Extents, Blöcken, Records und Bytes beschrie­ben ist, was mich bei den späteren DOS-​Dis­ketten nicht mehr sehr inter­essierte.

PIP-Optionen in Kapitel 9 (PIP-Funktionen), wo beschrieben wird, was man mit dem Peripheral Interchange Processor (PIP) alles machen konnte, wovon der COPY-Benutzer nur träumte.

Kurzübersicht über die BDOS-Funktionen in Kapitel 15 (Der CP/M-Kern: BDOS), wo ich oft nach­sehen mußte, wenn selbst geschrie­bene Pro­gramme eine BDOS-​Funk­tion aufrufen sollten. Denn nicht alles ging allein mit Hoch­sprachen, zumin­dest nicht schnell genug.

Diskettenbeschreiber und Verzeich­nisein­trag in Kapi­tel  15 (Der CP/M-Kern: BDOS), wo beschrie­ben ist, was in einem Ver­zeichnis-​Eintrag steht, damit auf der Diskette die richtigen Daten zur richtigen Datei gefunden werden.

[1] Bernd Pol: Vom Umgang mit CP/M. Erster und letzter Band der Reihe CP/M für die Praxis, IWT Verlag, 1982.

[2] Bernd Pol: Willkomen zu allerlei Text von Bernd Pol.

[3] Gaby Chaudry: Gaby's Homepage für CP/M und Computergeschichte.

Anfang und Ende

In letzter Zeit las ich bei einigen etwas über ihre elektronischen Erstenmale, ihren Erstkontakt mit Computern, Betriebssystemen, Programmen und Spielen, nicht aber Abstürzen, Verlusten und Viren. Dazu kamen mir drei Punkte in den Sinn:

1. Es ist oftmals schwierig, ein für allemal festzulegen, ab wann ein Zahlwort substantiviert benutzt wird und dann groß geschrieben oder gar getrennt werden muß, wozu ich mich nur manchmal durchringen kann. Mein Geschmack ist: "Das Erstemal war das letztemal, zu dem es kein weiteres Mal gab." Auf keinen Fall mogele ich mich heraus, indem ich leichtfertig oder ständig getrennt und groß schreibe: "Nun habe ich es mir sieben mal siebenundsiebzig mal gefallen lassen, beim nächsten Mal ist aber Schluß."
2. Wahrscheinlich ist die letzte Generation bereits eingeschult oder im Blog-Alter, die sich mit starken Gefühlen oder überhaupt an den ersten Umgang mit einem Computer, das erste beherrschte elektronische Spiel oder die wirklich verstandene Anwendung erinnern wird. Schon jetzt lese ich Notebook und Word als Erstkontakt. Danach können doch nur noch Erinnerungslücken kommen. So wird auf unabsehbare Zeit das Erstemal bleiben, was es immer war, und weder durch den ersten Computer, noch das erste Auto und schon gar nicht durch das zweite Leben ersetzt werden.
3. Mit zunehmendem Alter aber weiß man auch das letztemal zu schätzen. Ich höre schon den Einwand, man könne es doch gar nicht wissen. Tatsächlich wird mein jetziges Notebook wohl nicht das letzte sein, so Tag und Stunde, die auch junge Menschen nicht wissen, noch etwas auf sich warten lassen. Trotzdem weiß ich schon jetzt, welcher Rechner, welches Betriebssystem, welches Programm der oder das letzte war, den oder das ich wirklich verstanden habe. Sie laufen alle nur noch in Reservaten. Geblieben sind von ihnen neben schwachen Erinnerungen, endlosem Code und schlechten Bildern vor allem Bücher.

einmal ist keinmal
dutzendemal
zum x-ten Male

Erste-, Letzte- und Einzigemale
einzig verstandenes Betriebssystem CP/M
erster programmierter Rechner LOCI-2
einzig beherrschte Textverarbeitung Wordstar
einzig beherrschtes Computerspiel Adventure

Meine Vorhersage vor drei Monaten: 4,0%

Forderung der IG Metall      6,5%
Angebot der Arbeitgeber      2,5%

Rechnung: sqrt(6,5·2,5)=4,03

Erreichtes Ergebnis: effektiv 3,7% pro Jahr

4,1% und 1,7% bei 19 Monaten Laufzeit, also: (1,041·1,017)^(12/19)=1,0367

Erfolgsrechnung für Arbeitgeber: 2,9% im Jahr

4,1% in 2007 und 1,7% in 2008 oder später: (4,1+1,7)/2=2,9

Erfolg der Gewerkschaft: die 4 steht!

Erhöhung in 2007             4,1%
Erhöhung in 2008             1,7%
400 Euro einmalig (1)        1,0%
5 mal 0,7 Prozent (2)        0,3%
                             ----
in 19 Monaten Laufzeit       7,1%
im Jahr 12/19 davon          4,5%

(1) bei 40.000 Euro brutto im Jahr
(2) 0,7·(5/12)=0,29

Die 4 steht! Vor dem Komma der sofortigen 4,1 Prozent und vor den jähr­lichen 4,5 Prozent laut Rechnung!

Einführung in die kreative Mathematik

Mit 3,98 Prozent knapp verfehlt wird die 4 bei krea­tiver Umrech­nung der fünfmal 0,7 Prozent Einmal­zahlung im näch­sten Jahr. Das geht mit 13,65 Monats­gehäl­tern wie folgt: (5·0,7)·(13,65/12)=3,98. Ich habe nicht nur mit Arbeit­gebern, Gewerk­schaften und Banken, sondern mit vielen Menschen ein Problem: Sie können oder wollen oft nicht sagen, was die 100% sind.

Hier eine unausgegorene Aufgabe zu linearen Funktionen und ihre Darstellung, wenn ich mich einmal derart schlicht und direkt ausdrücken darf:

Der Graph einer linearen Funktion geht durch
die Punkte P(8|9) und Q(1|2).
a) Bestimme den Term einer proportionalen Funktion,
   deren Graph parallel zu dem Graphen von f ist.
b) Bestimme den Term der linearen Funktion h,
   deren Graph parallel zu dem Graphen von f ist
   und durch den Punkt R(2|-3) geht.

Dem Mathematiker fällt reflexhaft die Bezugnahme auf eine nicht bezeichnete Funktion f auf, denkt sich aber sofort, daß wohl die lineare Funktion f durch die Punkte P und Q gemeint ist. Er setzt in Teil a der Aufgabe sofort eine propor­tio­nale Funktion g an und wundert sich somit nicht über das Erscheinen von h im Teil b. Auf der anderen Seite bemerken selbst Schul­buch­autoren gar nicht die Unbe­stimmtheit von f und wundern sich auch nicht über das Fehlen von g, obgleich doch von f und h die Rede ist. Und Lehrer stehen auf dem Schlauch, wenn Schüler sie um eine Erläu­terung bitten. Zur Schul­buch­kritik oder Streichung der Aufgabe fehlt es oft an Souve­ränität.

Wer das so liest, könnte mich für pingelig halten, sollte aber beachten, daß er möglicher­weise den kleinen Schwach­punkt ohne meine Erläu­terung einfach über­sehen hätte oder bei der Lösung an ganz anderen Kleinig­keiten geschei­tert wäre, zum Beispiel an dem feinen Unter­schied zwischen linear und propor­tional oder an dem breiten Graphen-Geschwafel. Selbst­verständ­lich können nicht nur Mathe­matiker solche leichten Schwächen korri­gieren, und es wäre mir auch lieb, wenn in der Schule eine derartige Fehler­toleranz geübt würde, auf daß jeder Abitu­rient in der Lage wäre, auch sehr formale Sach­verhalte weit­gehend in geläu­figer Umgangs­sprache exakt zu beschreiben. Doch leider sehe ich eher das Gegenteil: In der Schul­mathe­matik werden Begriffe und Bezeich­nungen eingeführt, die in der wirklichen Mathematik unge­bräuchlich oder einfach unsinnig sind, um mich anderer Vokabeln zu enthalten. Auch das demon­striert die eingangs erwähnte Aufgabe.

Dem flüchtigen Leser wird "die Punkte P(8|9) und Q(1|2)" gar nicht irritieren. Ich aber frage mich, was an der tradi­tionellen Schreib­weise "die Punkte P=(8,9) und Q=(1,2)" auszusetzen ist. Etwa die Gleich­setzung der Punkte P und Q mit den Paaren (8,9) und (1,2)? Soll der senk­rechte Strich irgend­etwas andeuten? Daß es sich um Koor­dinaten handelt? Soll P(8|9) etwa für "Punkt P mit Abszisse 8 und Ordinate 9" stehen? Oder gar für den Punkt mit den Koor­dinaten 8 und 9? Nein, letzteres geht nicht, dann wäre Q(1,2) ja ein Qunkt! Wahr­scheinlich soll z(x|y) eine triviale Relation über E×R×R sein, die immer dann erfüllt ist, wenn der Punkt z der Ebene E die Koor­dinaten x und y hat, obgleich dann P und Q die Punkte wären, nicht P(8|9) und Q(1|2). Und da man diese Ungereimt­heiten einem Acht­kläßler zu erklären nicht in der Lage ist, bleibt wieder einmal kritik­lose Aneignung von Schul­konven­tionen, wo schlichtes Verstehen so einfach wäre.

Liste aller Hausaufgaben