Logarithmentafel
wuerg, 29.07.2006 16:22
Wer sich für Rechenschieber interessiert, kennt gewiß auch noch Logarithmentafeln, die immer dann erforderlich wurden, wenn mit höherer Genauigkeit zu rechnen war und die vier Grundrechenarten der elektromechanischen Tischrechner nicht ausreichten. Mit ihnen konnte man zwar schön Wurzelziehen und abartige Potenzen wie π hoch π genauer ausrechnen, doch waren für kompliziertere Rechnungen weitere Funktionstafeln erforderlich. Vor allem solche für die trigonometrischen Funktionen.
Moderne Tafeln sind vom Computer erstellt, also errechnet und gesetzt. Das war früher nicht so. Ab 1960 aber wurden sie auch nicht mehr durch Rechenkünstler kalkuliert, sondern von ausgedruckten Tabellen abgeschrieben. Und so besitze ich noch eine ordentlich gesetzte Tafel aus dem Jahre 1963 von F. G. Gauß, nicht C. F. Gauß. Im Vergleich zu anderen Büchern dieser Zeit ist es mit 5 Euro nur wenig wert. Ich erlaube mir ein paar kleine Auszüge aus diesem Werk, jedoch zur Schonung meiner Startseite in den Kommentaren.
Rechenschieber
Moderne Tafeln sind vom Computer erstellt, also errechnet und gesetzt. Das war früher nicht so. Ab 1960 aber wurden sie auch nicht mehr durch Rechenkünstler kalkuliert, sondern von ausgedruckten Tabellen abgeschrieben. Und so besitze ich noch eine ordentlich gesetzte Tafel aus dem Jahre 1963 von F. G. Gauß, nicht C. F. Gauß. Im Vergleich zu anderen Büchern dieser Zeit ist es mit 5 Euro nur wenig wert. Ich erlaube mir ein paar kleine Auszüge aus diesem Werk, jedoch zur Schonung meiner Startseite in den Kommentaren.
Rechenschieber
... comment
wuerg,
29.07.2006 16:24
Schon mit der Überschrift hat man sich früher mehr Mühe gegeben:

Fünf- und siebenstellige Logarithmen (jpg)
Und auch die Tafeln waren noch schön umrandet:
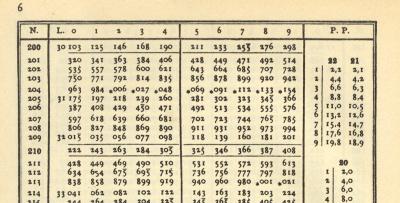
Tafel samt partes proportionales (jpg)

Fünf- und siebenstellige Logarithmen (jpg)
Und auch die Tafeln waren noch schön umrandet:

Tafel samt partes proportionales (jpg)
... link
kid37,
01.08.2006 23:56
Schön gesetzt. Ich bin ja auch noch mit so einer (wenig schön gestalteten) Sammlung zum Mathematikunterricht. Vermutlich benutzt man heute nur noch den Taschenrechner?
... link
... comment
wuerg,
04.08.2006 00:52
Mit Logarithmen kann man zwar schön multiplizieren, dividieren, potenzieren und auch Wurzeln ziehen, doch schon bei den trigonometrischen Funktionen nützen sie leider nicht viel. Deshalb gab es ergänzende Tafeln für Sinus und Tangens, meist auch für Kosinus und Kotangens, doch nur selten für Sekans und Kosekans:

Logarithmen der trigonometrischen Funktionen (jpg)
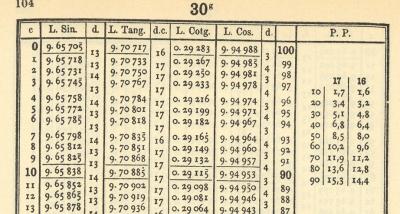
Tafel ab 30 Neugrad (jpg)
Dem aufmerksamen Betrachter fällt vielleicht dreierlei auf: Es werden nicht die Werte der trigonometrischen Funktionen, sondern ihre Logarithmen angegeben. Das ist von Vorteil, wenn man mit Logarithmen rechnet, weil die trigonometrischen Funktionen nur selten addiert, aber sehr gerne multipliziert werden.

Logarithmen der trigonometrischen Funktionen (jpg)

Tafel ab 30 Neugrad (jpg)
Dem aufmerksamen Betrachter fällt vielleicht dreierlei auf: Es werden nicht die Werte der trigonometrischen Funktionen, sondern ihre Logarithmen angegeben. Das ist von Vorteil, wenn man mit Logarithmen rechnet, weil die trigonometrischen Funktionen nur selten addiert, aber sehr gerne multipliziert werden.
... link
... comment
wuerg,
04.08.2006 23:31
Jetzt habe ich fast gehofft, irgendeiner hätte an 1/2 für den Sinus von 30 Grad erinnert, aus der ersten hier abgebildeten Tafel den Logarithmus von 2 als 0,30103 abgelesen und gefolgert, daß
lg (sin 30°) = lg (1/2) = −lg 2 = −0,30103 = 9,69897−10
ist und nicht wie in der zweiten Tafel angegeben 9,65705−10. So muß ich ohne diesen Einwand die Teilung der Tafel in Neugrad erwähnen. Und tatsächlich ist
lg (sin 30g) = lg (sin 27°) = 9,65705−10
wie Bill Gates sein Rechner schneller und genauer anzeigt. Warum hatte ich mir seinerzeit eine Tafel in neuer Teilung gekauft? Wahrscheinlich dachte ich, sie würde sich durchsetzen. Doch das trat nicht ein. Der rechte Winkel hat immer noch 90 Grad und nicht 100, die Stunde 60 Minuten und ebenfalls keine 100. Und das ist gut so.
lg (sin 30°) = lg (1/2) = −lg 2 = −0,30103 = 9,69897−10
ist und nicht wie in der zweiten Tafel angegeben 9,65705−10. So muß ich ohne diesen Einwand die Teilung der Tafel in Neugrad erwähnen. Und tatsächlich ist
lg (sin 30g) = lg (sin 27°) = 9,65705−10
wie Bill Gates sein Rechner schneller und genauer anzeigt. Warum hatte ich mir seinerzeit eine Tafel in neuer Teilung gekauft? Wahrscheinlich dachte ich, sie würde sich durchsetzen. Doch das trat nicht ein. Der rechte Winkel hat immer noch 90 Grad und nicht 100, die Stunde 60 Minuten und ebenfalls keine 100. Und das ist gut so.
... link
... comment
wuerg,
09.08.2006 01:06
Es soll ja nicht der Eindruck entstehen, vor 40 Jahren hätten wir alle hinter dem Mond gelebt, weil es noch keinen PC gab. Wohl aber schon eine [1] IBM 650, mit der die von Karl Rottmann herausgegebenen siebenstelligen Logarithmen berechnet wurden. Und in einem naturgemäß etwas dickeren Band dann auf einer IBM 704 auch die der trigonometrischen Funktionen. Das war im Jahre 1961, und die Zahlen stimmen immer noch:
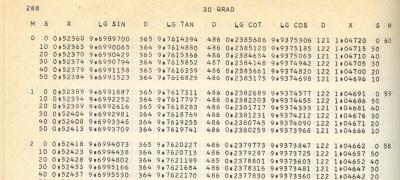
Tafel ab 30 Altgrad (jpg)
[1] Ja damals waren die Rechner noch Maschinen und weiblich.

Tafel ab 30 Altgrad (jpg)
[1] Ja damals waren die Rechner noch Maschinen und weiblich.
... link
wuerg,
09.08.2006 21:22
Manchmal sind die trigonometrischen Funktionen doch ohne Logarithmus günstiger. Oder man möchte einfach nur Gradangaben ins Bogenmaß wandeln oder umgekehrt:
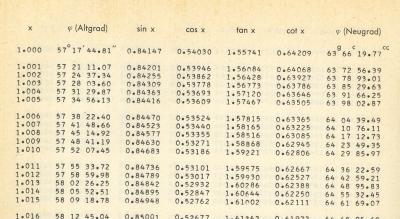
Tafel im Bogenmaß (jpg)
Und so liegt es auf der Hand, auch gleich die Hyperbelfunktionen und deren Basis, die auf- und absteigende Exponentialfunktion, in Tabellenform zu haben:
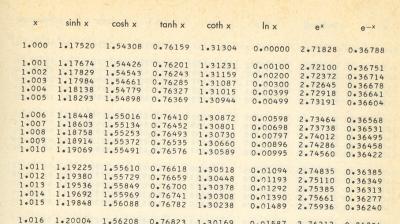
Hyperbelfunktionen (jpg)
Doch damit nicht genug. Auch die elementaren Funktionen sind ohne Taschenrechner ein Problem. Dagegen helfen ebenfalls Tafeln:
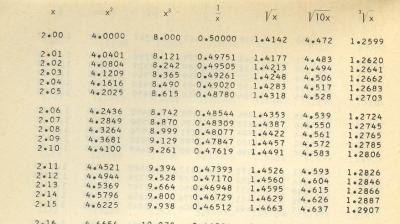
Elementarfunktionen (jpg)

Tafel im Bogenmaß (jpg)
Und so liegt es auf der Hand, auch gleich die Hyperbelfunktionen und deren Basis, die auf- und absteigende Exponentialfunktion, in Tabellenform zu haben:

Hyperbelfunktionen (jpg)
Doch damit nicht genug. Auch die elementaren Funktionen sind ohne Taschenrechner ein Problem. Dagegen helfen ebenfalls Tafeln:

Elementarfunktionen (jpg)
... link
... comment
