311
wuerg, 07.05.2008 00:55
Zu jeder Zahl kann ermittelt werden, auf wieviele Arten sie als Summe aufeinanderfolgender Primzahlen geschrieben werden kann. Und es liegt die Frage auf der Hand, welche die kleinste Zahl zu einer vorgegebenen Anzahl von Zerlegungen ist. [1] So kann die 41 auf dreifache Art als Summe von Primzahlen in Folge geschrieben werden, nämlich als 3+5+7+11+13, als 11+13+17 und als 41 allein. Und 41 ist die kleinste Zahl mit dieser Eigenschaft. Für exakt 1, 2, 3, 4 und 5 Summanden erhält man als kleinste Summe 2, 5, 41, 1151 und 311:
Das ist zwar keine Eigenschaft mit irgendeinem praktischen Nutzen, dennoch aber eine von allgemeiner Bedeutung, daß sie Besuchern aus dem Weltraum zwar nicht geläufig, aber bekannt sein wird. Das unterscheidet von irdischen Beliebigkeiten: Der 311 als amerikanische Nicht-Notruf-Nummer im Gegensatz zur 911. Dem Anschlag in Madrid (3/11/2004) im Gegensatz zu dem in New York (9/11/2001). Oder der Verdreifachung des 11. Buchstabens K zu KKK, nicht für „Kinder, Küche, Kirche“ sondern für den Ku Klux Klan.
[1] The On-Line Encyclopedia of Integer Sequences. Anzahl der Zerlegungen A054845 einer Zahl als Summe aufeinanderfolgender Primzahlen und kleinste Zahl A054859 einer vorgegebenen Anzahl von Zerlegungen.
1 2 3 4 5
2 5 41 1151 311
2+3 11+13+17 379+383+389 101+103+107
2+3+5+7+11+13 223+227+229+233+239 53+59+61+67+71
7+11+13+...+89+97+101 31+37+41+43+47+53+59
11+13+17...+41+43+47
Darunter ist die Zahl 311 deshalb bemerkenswert, weil sie mit fünf Zerlegungen deutlich kleiner ist als 1151 mit nur vieren.Das ist zwar keine Eigenschaft mit irgendeinem praktischen Nutzen, dennoch aber eine von allgemeiner Bedeutung, daß sie Besuchern aus dem Weltraum zwar nicht geläufig, aber bekannt sein wird. Das unterscheidet von irdischen Beliebigkeiten: Der 311 als amerikanische Nicht-Notruf-Nummer im Gegensatz zur 911. Dem Anschlag in Madrid (3/11/2004) im Gegensatz zu dem in New York (9/11/2001). Oder der Verdreifachung des 11. Buchstabens K zu KKK, nicht für „Kinder, Küche, Kirche“ sondern für den Ku Klux Klan.
[1] The On-Line Encyclopedia of Integer Sequences. Anzahl der Zerlegungen A054845 einer Zahl als Summe aufeinanderfolgender Primzahlen und kleinste Zahl A054859 einer vorgegebenen Anzahl von Zerlegungen.
... comment
regenblau,
07.05.2008 22:09
Zahlenspielerei
Ich bin kein Mathematikgenie, nein das nicht. Aber sowas ist schön zu lesen.
... link
... comment
wuerg,
08.05.2008 01:05
Viele werden sich weigern, eine Summe aus nur einem Summanden als solche anzuerkennen. Nicht nur für sie gibt es natürlich auch eine Aufstellung [1] der kleinsten Zahlen mit einer vorgegebener Anzahl echter Zerlegungen [2]:
Anders steht es um die 41. Als Primzahl bleiben ihr von den drei Zerlegungen nur zwei echte. Dadurch erhalten kleinere Zahlen die Chance auf ebenfalls zwei, die als kleinste von der 36 wahrgenommen wird. Das gleiche Schicksal erleidet die 1151. Von den vier Zerlegungen bleiben drei echte. Aber das schafft die kleinere 240 auch.
[1] Wie auch im Hauptbeitrag ehemals als eine schöne Tabelle mit Umrandung. Doch eines Tages wurde aus welchem Grunde auch immer <table> einfach entfernt, sobald man nacheditierte.
[2] The On-Line Encyclopedia of Integer Sequences. Anzahl der echten Zerlegungen A084143 einer Zahl als Summe aufeinanderfolgender Primzahlen und kleinste Zahl A067376 einer vorgegebenen Anzahl von Zerlegungen.
1 2 3 4 5
5 36 240 311 16277
2+3 17+19 113+127 101+103+107 2297+2309+...+2339+2341
5+7+11+13 53+59+61+67 53+59+61+67+71 1451+1453+...+1499+1511
17+19+23+29+31+37+41+43 31+37+...+53+59 1231+1237+...+1303+1307
11+13+...+43+47 359+367+373+...+571+577
331+337+347+...+557+563
Wieder ist 311 dabei, weil diese Primzahl ja gut auf ihre triviale Zerlegung verzichten kann. Sie hat dann zwar nur noch vier echte Zerlegungen statt fünf insgesamt, doch wissen wir bereits, daß alle Zahlen unterhalb von 311 maximal drei Zerlegungen aufweisen, also keine vier und schon gar keine echten.Anders steht es um die 41. Als Primzahl bleiben ihr von den drei Zerlegungen nur zwei echte. Dadurch erhalten kleinere Zahlen die Chance auf ebenfalls zwei, die als kleinste von der 36 wahrgenommen wird. Das gleiche Schicksal erleidet die 1151. Von den vier Zerlegungen bleiben drei echte. Aber das schafft die kleinere 240 auch.
[1] Wie auch im Hauptbeitrag ehemals als eine schöne Tabelle mit Umrandung. Doch eines Tages wurde aus welchem Grunde auch immer <table> einfach entfernt, sobald man nacheditierte.
[2] The On-Line Encyclopedia of Integer Sequences. Anzahl der echten Zerlegungen A084143 einer Zahl als Summe aufeinanderfolgender Primzahlen und kleinste Zahl A067376 einer vorgegebenen Anzahl von Zerlegungen.
... link
... comment
wuerg,
09.05.2008 21:31
Hier noch einmal eine Zusammenstellung der kleinsten Zahlen mit vorgegebener Anzahl von Zerlegungen:
k kleinste Zahl mit genau k Zerlegungen
alle Zerleg echte Zerleg Faktoren
0 1 1 1,0
1 2 5 2,5 3,2
2 5 36 7,2 4,2
3 41 240 5,9 7,4
4 1151 311 0,3 6,0
5 311 16277 52,3 3,8
6 34421 130638 3,8 29,8
7 218918 218918 1,0 3,3
8 3634531 9186778 2,5 26,4
9 48205429 556259425 11,5 28,3
10 1798467197 611108324 2,6 17,6
11 12941709050 12941709050 1,0 4,5
12 166400805323 12,9
13 6123584726269 36,8
Im Mittel sind die kleinsten Zahlen zu echten Zerlegungen etwa dreimal so groß wie die zu allen (1. Faktor), und mit jeder Zeile weisen sie eine Stelle mehr auf (2. Faktor). Ob ersteres so bleibt, weiß ich nicht. Letzteres aber sicherlich nicht. Daß gelegentlich nebeneinander zwei gleiche Zahlen wie 218918 stehen, ist durchaus zu erwarten. Ist die kleinste Zahl mit genau k Zerlegungen nämlich zusammengesetzt, ist sie auch die kleinste mit genau k echten Zerlegungen. Ebenso normal sind zwei gleiche Zahlen wie 5 und 311 längs der Diagonalen. Möglicherweise gibt es auch in den unbekannten Tiefen der Fortsetzung der Tabelle noch eine zweite Zahl wie 311, deren Vorgänger sogar größer ist.... link
... comment
wuerg,
18.05.2008 00:54
Eine naheliegende Frage lautet: In welchen Maße wächst die kleinste Zahl mit der Anzahl der vorgegebenen Zerlegungen? Dazu habe ich einmal die Trefferdichte überschlagen. Um die Zahl n herum haben die Primzahlen einen mittleren Abstand von lnn=1⋅ln(n/1), für die Summen zweier Primzahlen ist er 2⋅ln(n/2), für die aus dreien 3⋅ln(n/3) usw. Summiert man deren Kehrwerte, ergibt sich eine mit wachsendem n gegen ln2=0,693 gehende Trefferdichte. [1] Die Verhältnisse liegen zumindest für große n wie folgt:
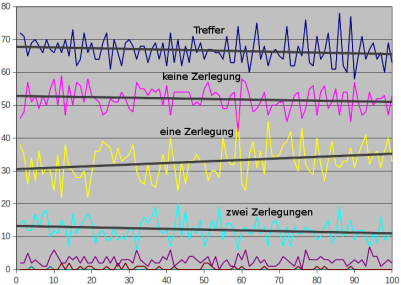
Treffer r und Anzahlen p(k) in hundert Hunderterblöcken bis 10.000 (png)
Wenn dieses Diagramm und meine Berechnungen mich nicht täuschen, sollte die Wahrscheinlichkeit, daß die kleinste Zahl mit k Zerlegungen kleiner ist als die mit k−1 etwa 1/k sein. Unterhalb von 12 liegt mit 311 bei k=5 die einzig bekannte Umkehr der Reihenfolge. Im Bereich von 12 bis 100 ist mit zwei weiteren zu rechnen. Vielleicht werden leistungsfähige Rechner in Haushalten von Fanatikern bald eine davon finden.
Aber zurück zur Eingangsfrage, in welchem Maße die kleinsten Zahlen mit wachsender Trefferzahl größer werden. Die Tabelle
[1] Das hatte ich so lax hingeschrieben. Der aufmerksame Leser wird bemerkt haben, daß spätesten mit k=n der Nenner 0 wird. Natürlich soll nur für solche k summiert werden, für die die Summe der ersten k Primzahlen n nicht übersteigt. In [3] ist bewiesen, in welchem Sinne ln2 tatsächlich korrekt ist.
[2] Eine genauere Rechnung sollte natürlich auf anfänglich fallende Trefferraten führen, da mein Diagramm bis 10.000 das nahelegt und ein Programm die Summe der 1/(k⋅ln(n/k)) bis etwa 500 Millionen tatsächlich auf 0,6444 fallen läßt. Erst danach ziehen sie wieder an. Die gegen die Erwartung verlaufenden Entwicklungen der Anzahlen ohne bzw. mit einfacher Zerlegung mag man als eine Angleichung einer anfänglichen Abweichung an die großen Zahlen sehen, doch schießen beide schon bald über das Ziel hinaus.
[3] L. Moser: On The Sum of Consecutive Primes. Canadian Mathematical Bulletin 6/2, 2018. Ist aₙ=A054845(n) die Anzahl der Zerlegungen von n als Summe aufeinanderfolgender Primzahlen, so konvergiert (a₁+a₁+…+aₙ)/n gegen ln2.
r = ln2 = 69% Trefferdichte p(0) = e−r = 1/2 = 50% haben keine Zerlegung p(1) = r⋅p(0) = 35% haben eine Zerlegung p(2) = r⋅p(1)/2 = 12% haben zwei Zerlegungen p(3) = r⋅p(2)/3 = 3% haben drei ZerlegungenDas sind die Ergebnisse einer Überschlagsrechnung, die unberücksichtigt läßt, daß die Treffer nicht wirklich unabhängig fallen. Es ist deshalb nicht selbstverständlich, daß schon bei kleinen Zahlen die errechneten Werte einigermaßen getroffen werden:

Treffer r und Anzahlen p(k) in hundert Hunderterblöcken bis 10.000 (png)
Wenn dieses Diagramm und meine Berechnungen mich nicht täuschen, sollte die Wahrscheinlichkeit, daß die kleinste Zahl mit k Zerlegungen kleiner ist als die mit k−1 etwa 1/k sein. Unterhalb von 12 liegt mit 311 bei k=5 die einzig bekannte Umkehr der Reihenfolge. Im Bereich von 12 bis 100 ist mit zwei weiteren zu rechnen. Vielleicht werden leistungsfähige Rechner in Haushalten von Fanatikern bald eine davon finden.
Aber zurück zur Eingangsfrage, in welchem Maße die kleinsten Zahlen mit wachsender Trefferzahl größer werden. Die Tabelle
k Zahlen mit genau k Zerlegungen
kleinste alle wieviel
0 1 2
1 2 3
2 5 8
3 41 36
4 1.151 200
5 311 1.500
6 34.421 13.000
7 218.918 130.000
8 3.634.531 1.500.000
9 48.205.429 20.000.000
10 1.798.467.197 280.000.000
11 12.941.709.050 4.500.000.000
12 166.400.805.323 78.000.000.000
gibt die bekannten kleinsten Zahlen und dahinter die zu erwartenden Abstände zwischen Zahlen mit der vorgegebenen Trefferzahl n an. Die Tabelle und mein Diagramm legen statt ln2=0,693 eine etwas kleinere Trefferrate von etwa 0,65 nahe. Und so entstehen aus einer Antwort wieder einmal fünf Fragen: Führt genauere Rechnung für kleine n auf eine fallende Trefferrate r unterhalb von ln2? Warum sind die trefferlosen Zahlen zunächst häufiger als gemäß der Trefferrate zu erwarten? Warum fällt ihr Anteil trotz geringerer Trefferrate? Warum sind die Einzeltreffer zunächst seltener als zu erwarten? Warum steigt ihr Anteil gegen die Erwartung? [2][1] Das hatte ich so lax hingeschrieben. Der aufmerksame Leser wird bemerkt haben, daß spätesten mit k=n der Nenner 0 wird. Natürlich soll nur für solche k summiert werden, für die die Summe der ersten k Primzahlen n nicht übersteigt. In [3] ist bewiesen, in welchem Sinne ln2 tatsächlich korrekt ist.
[2] Eine genauere Rechnung sollte natürlich auf anfänglich fallende Trefferraten führen, da mein Diagramm bis 10.000 das nahelegt und ein Programm die Summe der 1/(k⋅ln(n/k)) bis etwa 500 Millionen tatsächlich auf 0,6444 fallen läßt. Erst danach ziehen sie wieder an. Die gegen die Erwartung verlaufenden Entwicklungen der Anzahlen ohne bzw. mit einfacher Zerlegung mag man als eine Angleichung einer anfänglichen Abweichung an die großen Zahlen sehen, doch schießen beide schon bald über das Ziel hinaus.
[3] L. Moser: On The Sum of Consecutive Primes. Canadian Mathematical Bulletin 6/2, 2018. Ist aₙ=A054845(n) die Anzahl der Zerlegungen von n als Summe aufeinanderfolgender Primzahlen, so konvergiert (a₁+a₁+…+aₙ)/n gegen ln2.
... link
... comment
dhonau,
23.05.2008 22:30
ich nenne ...
das prinzip der primzahlen
eine minimalisierung in der wiederholung und eine maximalisierung in der streuung von elementen abzählbar unendlicher welten (mengen)
ich habe mich mit primzahlen ein wenig beschäftigt
obige philosophische (arbeitshypo-)these ist mehr oder weniger intuitiver natur
eine minimalisierung in der wiederholung und eine maximalisierung in der streuung von elementen abzählbar unendlicher welten (mengen)
ich habe mich mit primzahlen ein wenig beschäftigt
obige philosophische (arbeitshypo-)these ist mehr oder weniger intuitiver natur
... link
wuerg,
24.05.2008 00:05
Eigentlich will ich mich gar nicht so sehr über Primzahlen auslassen, denn das wenige, was ich über sie weiß, kann man vielerorts genauer und besser beschrieben nachlesen. Aber mit der Zahl 311 habe ich mich etwas in den Primzahlsummen verfangen und muß nun eine Weile rechnen, bevor ich wieder davon lassen kann.
... link
... comment
wuerg,
24.05.2008 16:38
Die erste Schlußfrage meines vorangehenden Kommentares lautete: Warum bleibt die Trefferrate zumindest unterhalb von 10000 deutlich hinter ln2=0,693 zurück und fällt zu Beginn sogar ab?
Zur Antwort muß etwas genauer gerechnet werden. Gehe ich weiterhin davon aus, daß um die Zahl n herum die Summen aus k Primzahlen in Folge einen mittleren Abstand von k⋅ln(n/k) haben, ergibt sich eine Gesamttrefferquote von
r(n) = 1/(1⋅ln(n/1)) + + … + 1/(m·ln(n/m))
worin m so gewählt wird, daß die Summe der ersten m Primzahlen gerade noch unter n bleibt. Das ist ungefähr bei
n = (m/2)⋅lnm oder m = 2⋅√(n/lnn)
der Fall und führt letztlich auf die Näherung
r(n) = ln2 + (2−lnlnn)/lnn
Bis n um 1600 (e hoch e hoch 2) liegt r(n) oberhalb von ln2=0,693 und fällt bis etwa 500 Millionen (e hoch e hoch 3) ganz langsam auf etwa 0,643 ab. Erst danach steigt r(n) wieder gegen den Zielwert ln2=0,693. Das steht im Einklang mit dem Verlauf der von mir bis n=10000 gezählten Treffer und auch einem Programm, daß bis 10 hoch 18 die Summe der 1/(k⋅ln(n/k)) berechnet.
Damit ist wenigstens eine Frage einigermaßen beantwortet, und ich will diesmal nur eine weitere Folgefrage erwähnen: Warum bleiben die ermittelten Werte dennoch hinter den errechneten zurück? Von 1001 bis 2000 zähle ich 676 Treffer, das sind 19 weniger als r(1500)=0,695 erwarten läßt. Von 8001 bis 9000 sind es 659 und damit 12 weniger. Die Abweichung scheint abzunehmen. Doch ist das wirklich der Fall? Ein mir bekanntes Ergebnis [1] spricht dagegen: Bis 260 Milliarden gibt es 5722 Neunfach-Treffer, was nach der Beziehung
5722 / 260.000.000.000 = (r9/9!)⋅e−r
auf eine Trefferrate von r=0,628 schließen läßt. Das sind fast drei Prozent weniger als mit der Näherungsformel zu erwarten.
Und für den einen, der wirklich nachrechnet, sage ich es gleich: Die 2 aus dem Korrekturterm (2−lnlnn)/lnn ist von mir großzügig gerundet. Sie steht für c(n)+2log2 worin c(n) ausgleicht, was bei der Ersetzung der Summe durch ein Integral verschlappert wird. Naturgemäß liegt dieser Wert für große n in der Nähe der Euler-Mascheroni-Konstanten. Ich habe ihn großzügig mit 0,614 statt 0,577 angesetzt, um auf 2 zu kommen.
[1] Carlos Rivera: Puzzle 46.- Primes expressible as sum of consecutive primes in K ways.
Zur Antwort muß etwas genauer gerechnet werden. Gehe ich weiterhin davon aus, daß um die Zahl n herum die Summen aus k Primzahlen in Folge einen mittleren Abstand von k⋅ln(n/k) haben, ergibt sich eine Gesamttrefferquote von
r(n) = 1/(1⋅ln(n/1)) + + … + 1/(m·ln(n/m))
worin m so gewählt wird, daß die Summe der ersten m Primzahlen gerade noch unter n bleibt. Das ist ungefähr bei
n = (m/2)⋅lnm oder m = 2⋅√(n/lnn)
der Fall und führt letztlich auf die Näherung
r(n) = ln2 + (2−lnlnn)/lnn
Bis n um 1600 (e hoch e hoch 2) liegt r(n) oberhalb von ln2=0,693 und fällt bis etwa 500 Millionen (e hoch e hoch 3) ganz langsam auf etwa 0,643 ab. Erst danach steigt r(n) wieder gegen den Zielwert ln2=0,693. Das steht im Einklang mit dem Verlauf der von mir bis n=10000 gezählten Treffer und auch einem Programm, daß bis 10 hoch 18 die Summe der 1/(k⋅ln(n/k)) berechnet.
Damit ist wenigstens eine Frage einigermaßen beantwortet, und ich will diesmal nur eine weitere Folgefrage erwähnen: Warum bleiben die ermittelten Werte dennoch hinter den errechneten zurück? Von 1001 bis 2000 zähle ich 676 Treffer, das sind 19 weniger als r(1500)=0,695 erwarten läßt. Von 8001 bis 9000 sind es 659 und damit 12 weniger. Die Abweichung scheint abzunehmen. Doch ist das wirklich der Fall? Ein mir bekanntes Ergebnis [1] spricht dagegen: Bis 260 Milliarden gibt es 5722 Neunfach-Treffer, was nach der Beziehung
5722 / 260.000.000.000 = (r9/9!)⋅e−r
auf eine Trefferrate von r=0,628 schließen läßt. Das sind fast drei Prozent weniger als mit der Näherungsformel zu erwarten.
Und für den einen, der wirklich nachrechnet, sage ich es gleich: Die 2 aus dem Korrekturterm (2−lnlnn)/lnn ist von mir großzügig gerundet. Sie steht für c(n)+2log2 worin c(n) ausgleicht, was bei der Ersetzung der Summe durch ein Integral verschlappert wird. Naturgemäß liegt dieser Wert für große n in der Nähe der Euler-Mascheroni-Konstanten. Ich habe ihn großzügig mit 0,614 statt 0,577 angesetzt, um auf 2 zu kommen.
[1] Carlos Rivera: Puzzle 46.- Primes expressible as sum of consecutive primes in K ways.
... link
... comment
wuerg,
31.05.2008 14:28
In meinem letzten Kommentar blieb ich eine Antwort auf die Frage schuldig, warum die wahre Trefferrate hinter der von mir errechneten um einige Prozente zurückbleibt. Neben falscher oder ungenauer Rechnerei, kommen mir zwei Ursachen in den Sinn. Zum einen liegen die Primzahlen und ihre Summen nicht zufällig. Zum anderen sind meine Ausgangsannahmen über ihre Dichte nicht hinreichend genau.
Für den mittleren Abstand der Zahlen aus k Summanden setzte ich k⋅ln(n/k) an, was von k etwa gleichgroßen Summanden der Größenordnung n/k ausgeht, in deren Nähe die Primzahlen den Abstand ln(n/k) aufweisen. Die unterschiedliche Größe der Summanden wirkt sich nur minimal und nach meinen Überlegungen auch in die andere Richtung aus.
Anders steht es um die wahre Dichte der Primzahlen [1]. Um 10.000 ist sie immer noch ein Prozent geringer als angesetzt. Doch im Bereich von 8001 bis 9000 sind zwei Prozent zu erklären. Dazu ist genauer hinzusehen: Bei n=8500 kommt man auf die maximale Summandenzahl von etwa m=2√(n/lnn)=61. Im Mittel sind es k=m/lnm=15, womit ein normaler Summand bei n/k=570 liegt, wo die wahre Dichte der Primzahlen durchaus die angesetzte um zwei Prozent unterschreitet.
Liegt n im Milliardenbereich, bleibt von diesem Effekt nur noch wenig übrig. Es muß also einen anderen Grund geben, weshalb bis 260 Milliarden nur 5722 Neunfachtreffer gezählt wurden, was einer Trefferrate von 62,8 statt der vorhergesagten 64,5 Prozent entspräche. Die verwendete Formel setzt Zufälligkeit voraus, von der man nicht unbedingt ausgehen kann, wenn die Zahl der infrage kommenden Objekte nicht sehr groß ist.
Feuert man nicht zufällig, sondern in einer einzigen Salve von 7 Schuß, so fallen auch 7 tot um. Die Wahrscheinlichkeit für 0 Treffer wäre 30 Prozent. Die in die Nähe einer Zahl treffenden Primzahlsummen entsprechen mehrerer solche Salven. Deshalb zeigt die vierte Spalte 3 Salven zu 3, 2 und 2 Schuß. Die Überlebensrate sinkt abermals, und mehr als dreimal kann keiner getroffen werden. Zum Ausgleich steigt die Zahl der Einzeltreffer erneut an.
Doch die Primzahlsalven treffen nicht nebeneinander, sondern in ungefähr gleichenbleibenden Abständen. In meinem Beispiel habe ich für die drei Salven die Abstände 2, 4 und 4 angesetzt. Die fünfte Spalte zeigt das Ergebnis. Der Salveneffekt wird teilweise aufgehoben.
Langer Rede kurzer Sinn: Das Beispiel soll deutlich machen, daß die Rate der Neunfachtreffer bis 260 Milliarden möglicherweise nicht einfach berechnet werden kann, als würde völlig willkürlich 168 Milliarden mal hineingeschossen. Ihr Zurückbleiben um den Faktor zwei ist durchaus plausibel.
Für den mittleren Abstand der Zahlen aus k Summanden setzte ich k⋅ln(n/k) an, was von k etwa gleichgroßen Summanden der Größenordnung n/k ausgeht, in deren Nähe die Primzahlen den Abstand ln(n/k) aufweisen. Die unterschiedliche Größe der Summanden wirkt sich nur minimal und nach meinen Überlegungen auch in die andere Richtung aus.
Anders steht es um die wahre Dichte der Primzahlen [1]. Um 10.000 ist sie immer noch ein Prozent geringer als angesetzt. Doch im Bereich von 8001 bis 9000 sind zwei Prozent zu erklären. Dazu ist genauer hinzusehen: Bei n=8500 kommt man auf die maximale Summandenzahl von etwa m=2√(n/lnn)=61. Im Mittel sind es k=m/lnm=15, womit ein normaler Summand bei n/k=570 liegt, wo die wahre Dichte der Primzahlen durchaus die angesetzte um zwei Prozent unterschreitet.
Liegt n im Milliardenbereich, bleibt von diesem Effekt nur noch wenig übrig. Es muß also einen anderen Grund geben, weshalb bis 260 Milliarden nur 5722 Neunfachtreffer gezählt wurden, was einer Trefferrate von 62,8 statt der vorhergesagten 64,5 Prozent entspräche. Die verwendete Formel setzt Zufälligkeit voraus, von der man nicht unbedingt ausgehen kann, wenn die Zahl der infrage kommenden Objekte nicht sehr groß ist.
Tref. 70Proz. 7aus10 3Salven mit Abstand 0 49,6% 47,8% 44,8% 45,8% 1 34,8% 37,2% 41,6% 40,9% 2 12,2% 12,4% 12,4% 12,5% 3 2,84% 2,30% 1,20% 1,36% 4 0,50% 0,26% keine keine 5 0,07% 0,02% keine keine 6 81ppm 6,3ppm keine keine 7 8,1ppm 0,1ppm keine keine 8 0,7ppm keine keine keineDie zweite Spalte der vorstehenden Tabelle zeigt einfach die Wahrscheinlichkeiten für Trefferzahlen der ersten, wenn in eine sehr große Zahl n von Objekten 0,7n mal völlig zufällig geschossen wird. In der dritten Spalte sind es nur n=10 Objekte und 7 Schuß. Naturgemäß sind Achtfachtreffer nicht mehr möglich und die Wahrscheinlichkeiten für hohe Trefferzahlen geringer. Aber auch die Überlebenschance (t=0) fällt etwas ab, während im Gegenzuge die Rate der Einzeltreffer steigt. Insgesamt ist der Effekt aber nicht berauschend, obwohl n=10 doch so klein ist.
Feuert man nicht zufällig, sondern in einer einzigen Salve von 7 Schuß, so fallen auch 7 tot um. Die Wahrscheinlichkeit für 0 Treffer wäre 30 Prozent. Die in die Nähe einer Zahl treffenden Primzahlsummen entsprechen mehrerer solche Salven. Deshalb zeigt die vierte Spalte 3 Salven zu 3, 2 und 2 Schuß. Die Überlebensrate sinkt abermals, und mehr als dreimal kann keiner getroffen werden. Zum Ausgleich steigt die Zahl der Einzeltreffer erneut an.
Doch die Primzahlsalven treffen nicht nebeneinander, sondern in ungefähr gleichenbleibenden Abständen. In meinem Beispiel habe ich für die drei Salven die Abstände 2, 4 und 4 angesetzt. Die fünfte Spalte zeigt das Ergebnis. Der Salveneffekt wird teilweise aufgehoben.
Langer Rede kurzer Sinn: Das Beispiel soll deutlich machen, daß die Rate der Neunfachtreffer bis 260 Milliarden möglicherweise nicht einfach berechnet werden kann, als würde völlig willkürlich 168 Milliarden mal hineingeschossen. Ihr Zurückbleiben um den Faktor zwei ist durchaus plausibel.
... link
... comment
wuerg,
23.06.2008 00:10
Aus einem vorangehenden Kommentar ist noch die Frage offen, warum im kleinzahligen Bereich die Anzahl der Einzeltreffer deutlich hinter der Erwartung zurückbleibt. So werden 680 Treffer im Bereich von 501 bis 1500 gezählt, was 344 bis 345 einfach getroffene Zahlen erwarten ließe. In Wirklichkeit sind es aber mit 306 deutlich weniger.
Von der 2 abgesehen sind alle Primzahlen ungerade. Somit bilden gerade Summandenzahlen fast immer gerade und ungerade immer ungerade Summen. Naturgemäß werden die geraden Zahlen (g) nicht so häufig getroffen wie die ungeraden (u):
g(n) ≈ r(n) − ln2/lnn
u(n) ≈ r(n) + ln2/lnn
Für n=1000 ist der Zu- bzw. Abschlag 0,1 in sehr guter Übereinstimmung mit den 292 geraden und den 388 ungeraden Treffern im Bereich von 501 bis 1500. Fielen sie in diesen beiden Zahlbereichen zufällig, so ergäben sich die Anteile der vierten Tabellenspalte. Das ist kein berauschender Schritt Richtung Realität. Deshalb die nächste Idee, auch noch die Primzahlen (p) von den übrigen ungeraden Zahlen (v) zu trennen. Das führt auf die Quoten der fünften Spalte, die sich von der Realität sogar noch etwas entfernen.
Viel stärker ist ein anderer Zusammenhang: Die Summen dreier Primzahlen treffen gerne wieder auf solche. Weil alle Primzahlen vom Typ 6k±1 sind, trifft dies auch für dreiviertel aller Summen aus drei Primzahlen zu. Die Dreifachsummen treffen also dreimal häufiger eine Primzahl wie der reine Zufall. Sehr oft führt die Summe dreier Primzahlen so zu keinen Einzeltreffern, sondern macht aus einem einzelnen einen doppelten. Normalerweise ergibt das zwei Einzeltreffer weniger. Zum Ausgleich sind es ein Doppeltreffer und eine nicht getroffene Zahl mehr.
Im Bereich von 501 bis 1500 gibt es 144 Primzahlen und 57 Dreifachsummen. Es wären also nur 8 Doppeltreffer aus beiden zu erwarten. Tatsächlich sind es mit 22 fast dreimal soviele. Gehe ich von 22−8=14 Doppeltreffern und Nichttreffern mehr sowie 14+14=28 Einfachtreffern weniger aus als der reine Zufall der Spalte zwei vorgibt, so komme ich auf die Wahrscheinlichkeiten der sechsten Spalte.
Das kommt der Realität schon recht nahe. Und es kommen ähnliche, wenn auch bescheidenere Effekte modulo größerer Zahlen als 6 hinzu, denen ich gerne den Rest zuschiebe. Sie genauer zu quantifizieren, erspare ich mir, denn diese Zusammenhänge sind nicht so wichtig wie eine Landung auf dem Mond, für dessen Bahnberechnung hunderte von Störungen zu berücksichtigen sind.
Tref. Zufall Realität u und g p,v,g mod 6 0 50,7% 52,7% 50,9% 49,8% 52,1% 1 34,4% 30,6% 34,4% 35,8% 31,6% 2 11,7% 13,3% 11,7% 11,7% 13,1% 3 2,6% 2,9% 2,7% 2,4% 2,6%Die Tabelle zeigt in der zweiten Spalte die zu erwartenden Trefferzahlen, wenn 680 mal völlig zufällig in den Tausenderblock geschossen würde. Die wahren Werte stehen in Spalte drei. Die Abweichung muß darin begründet sein, daß die Primzahlen und ihre Summen eben doch nicht zufällig fallen, was sich im kleinzahligen Bereich deutlich bemerkbar macht.
Von der 2 abgesehen sind alle Primzahlen ungerade. Somit bilden gerade Summandenzahlen fast immer gerade und ungerade immer ungerade Summen. Naturgemäß werden die geraden Zahlen (g) nicht so häufig getroffen wie die ungeraden (u):
g(n) ≈ r(n) − ln2/lnn
u(n) ≈ r(n) + ln2/lnn
Für n=1000 ist der Zu- bzw. Abschlag 0,1 in sehr guter Übereinstimmung mit den 292 geraden und den 388 ungeraden Treffern im Bereich von 501 bis 1500. Fielen sie in diesen beiden Zahlbereichen zufällig, so ergäben sich die Anteile der vierten Tabellenspalte. Das ist kein berauschender Schritt Richtung Realität. Deshalb die nächste Idee, auch noch die Primzahlen (p) von den übrigen ungeraden Zahlen (v) zu trennen. Das führt auf die Quoten der fünften Spalte, die sich von der Realität sogar noch etwas entfernen.
Viel stärker ist ein anderer Zusammenhang: Die Summen dreier Primzahlen treffen gerne wieder auf solche. Weil alle Primzahlen vom Typ 6k±1 sind, trifft dies auch für dreiviertel aller Summen aus drei Primzahlen zu. Die Dreifachsummen treffen also dreimal häufiger eine Primzahl wie der reine Zufall. Sehr oft führt die Summe dreier Primzahlen so zu keinen Einzeltreffern, sondern macht aus einem einzelnen einen doppelten. Normalerweise ergibt das zwei Einzeltreffer weniger. Zum Ausgleich sind es ein Doppeltreffer und eine nicht getroffene Zahl mehr.
Im Bereich von 501 bis 1500 gibt es 144 Primzahlen und 57 Dreifachsummen. Es wären also nur 8 Doppeltreffer aus beiden zu erwarten. Tatsächlich sind es mit 22 fast dreimal soviele. Gehe ich von 22−8=14 Doppeltreffern und Nichttreffern mehr sowie 14+14=28 Einfachtreffern weniger aus als der reine Zufall der Spalte zwei vorgibt, so komme ich auf die Wahrscheinlichkeiten der sechsten Spalte.
Das kommt der Realität schon recht nahe. Und es kommen ähnliche, wenn auch bescheidenere Effekte modulo größerer Zahlen als 6 hinzu, denen ich gerne den Rest zuschiebe. Sie genauer zu quantifizieren, erspare ich mir, denn diese Zusammenhänge sind nicht so wichtig wie eine Landung auf dem Mond, für dessen Bahnberechnung hunderte von Störungen zu berücksichtigen sind.
... link
... comment
wuerg,
05.07.2024 01:10
Nach 16 Jahren habe ich einiges, was ich hier anläßlich der Zahl 311 schrieb, nicht mehr so richtig verstanden. Bei der Überarbeitung mußte ich auf die alten Tabellen verzichten, da sie zwischenzeitlich von blogger.de munter ignoriert werden. Aber ich habe noch meine Zählung der Treffer bis 1.000.000 gefunden:
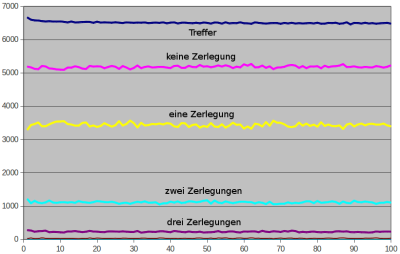
Treffer r und Anzahlen p(k) in hundert Zehntausenderblöcken bis 1.000.000 (png)
Das sieht schon viel ebenmäßiger aus als das Bild bis 10.000. Nur bleiben darin die Trefferraten trotz allem hinter ln2=0,693 zurück und fallen sogar leicht. Am rechten Rand, also im letzten Zehntausenderblock bis 1.000.000 stimmen die ermittelten 6481 Treffer sehr gut mit der geschätzten Rate von
r(n) = ln2 + (2−lnlnn)/lnn = 0,6931+0,1448−0,1901 = 0,6478
für n=995.000 überein. Bis etwa 500 Millionen wird r auf 0,643 noch etwas fallen. Danach geht es ganz, ganz langsam nach oben Richtung ln2=0,693. Bei einem Gogool (10 hoch 100) wird 0,678 erreicht.

Treffer r und Anzahlen p(k) in hundert Zehntausenderblöcken bis 1.000.000 (png)
Das sieht schon viel ebenmäßiger aus als das Bild bis 10.000. Nur bleiben darin die Trefferraten trotz allem hinter ln2=0,693 zurück und fallen sogar leicht. Am rechten Rand, also im letzten Zehntausenderblock bis 1.000.000 stimmen die ermittelten 6481 Treffer sehr gut mit der geschätzten Rate von
r(n) = ln2 + (2−lnlnn)/lnn = 0,6931+0,1448−0,1901 = 0,6478
für n=995.000 überein. Bis etwa 500 Millionen wird r auf 0,643 noch etwas fallen. Danach geht es ganz, ganz langsam nach oben Richtung ln2=0,693. Bei einem Gogool (10 hoch 100) wird 0,678 erreicht.
... link
... comment
